
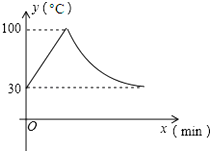 ���������ˮ����ͨ��Դ�ͽ�����ȳ���ˮ��ÿ��������10�棬���ȵ�100��ʱ�Զ��ػ���ˮ�¿�ʼ�½�����ʱˮ�£��棩��ʱ�䣨min���ɷ�������ϵ�������º㶨Ϊ30�棬��ˮ�½���30��ʱ���������ڶ��ּ��ȳ���ij�ּ��ȹ�����ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ��ʾ��
���������ˮ����ͨ��Դ�ͽ�����ȳ���ˮ��ÿ��������10�棬���ȵ�100��ʱ�Զ��ػ���ˮ�¿�ʼ�½�����ʱˮ�£��棩��ʱ�䣨min���ɷ�������ϵ�������º㶨Ϊ30�棬��ˮ�½���30��ʱ���������ڶ��ּ��ȳ���ij�ּ��ȹ�����ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ��ʾ������ ��1�����ɿ�������ʱˮ��ÿ��������10�棬�ɵô�30�浽100����Ҫ7���ӣ���һ�κ�����ϵʽΪ��y=k1x+b������0��30������7��100�����룬���ô���ϵ�������һ�κ����Ľ���ʽ���跴����������ϵʽΪ��y=$\frac{{k}_{2}}{x}$������7��100�����룬���ô���ϵ������������������Ľ���ʽ��
��2����y=50�ֱ����һ�κ����뷴�����Ľ���ʽ�����x��ֵ����������ɣ�
��� 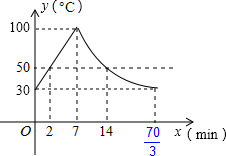 �⣺��1���߿�������ʱˮ��ÿ��������10�棬
�⣺��1���߿�������ʱˮ��ÿ��������10�棬
���30�浽100����Ҫ7���ӣ�
��һ�κ�����ϵʽΪ��y=k1x+b��
����0��30������7��100������y=k1x+b��k1=10��b=30��
��y=10x+30��0��x��7����
�跴����������ϵʽΪ��y=$\frac{{k}_{2}}{x}$��
����7��100�������k2=700��
��y=$\frac{700}{x}$��
��y=30���룬���x=$\frac{70}{3}$��
��y=$\frac{700}{x}$��7��x��$\frac{70}{3}$����
��2����y=50����y=10x+30�����x=2��
��y=50����y=$\frac{700}{x}$�����x=14��
14-2=12���֣���
����ij�ֹ�������12���ӵ�ʱ���ܽӵ�50�����ϵ�ˮ��
���� ������Ҫ������һ�κ�����������������Ӧ�ã��ؼ���Ҫ��ȷ�������⣬���ô���ϵ������������Ľ���ʽ��


 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Բ | B�� | ������ | C�� | Բ�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-4��2�� | B�� | ��-4��-2�� | C�� | ��4��-2�� | D�� | ��4��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
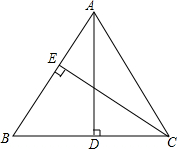 ��ͼ��AD��CE�ֱ��ǡ�ABC�б�BC��AB�ϵĸߣ���AD=10��CE=9��AB=12����BC�ij���
��ͼ��AD��CE�ֱ��ǡ�ABC�б�BC��AB�ϵĸߣ���AD=10��CE=9��AB=12����BC�ij����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com