
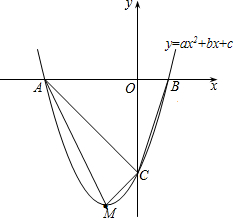
 如图,抛物线y=ax2+bx+c的开口向上,顶点M在第三象限,抛物线与x轴交于A、B 两点,与y轴负半轴交于点C,点A坐标为(-3,0),点B坐标为(1,0).
如图,抛物线y=ax2+bx+c的开口向上,顶点M在第三象限,抛物线与x轴交于A、B 两点,与y轴负半轴交于点C,点A坐标为(-3,0),点B坐标为(1,0).分析 (1)根据对称轴可得出a,b的关系,再把点(1,0)代入解析式即可得出a,c的关系;
(2)过点M作MN⊥y轴,S四边形AMCO=S梯形AMNO-S△CMN,从而用含有a的式子表示出△OCB与四边形AMCO的面积,再求比值即可;
(3)①过点M作MH⊥x轴,根据∠ACM=90°,得出AM2=AC2+CM2,AM2=AH2+MH2,AC2=OA2+OC2,CM2=CN2+MN2,分别用含有a的式子表示,计算即可得出a的值,再求得b,c的值,代入解析式,求得抛物线解析式,由OA=OC,可得∠OAC=∠OCA=45°,再由三角函数的定义得出tan∠MAC=$\frac{MC}{AC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,tan∠OCB=$\frac{OB}{OC}$=$\frac{1}{3}$,得出∠MAC=∠OCB,从而得出∠MAO=∠ACB;
②假设存在点D,使以点A、O、D为顶点的三角形与△ACB相似.先求得直线AM的解析式y=2x+6,再设出点D坐标(m,2m+6),分两种情况讨论:第一种情况△AOD∽△CAB;第二种情况△AOD∽△CBA;再得出比例式,第一种情况$\frac{OD}{AB}$=$\frac{AD}{CB}$,第二种情况$\frac{OD}{AB}$=$\frac{AO}{CB}$,再把数值代入即可得出m的值,根据-3≤m≤-1,进行取舍即可得出点D的坐标.
解答 解:(1)∵抛物线与x轴的交点为A(-3,0),B(1,0),
∴对称轴为直线x=-1,
∴-$\frac{b}{2a}$=-1,
∴b=2a,
把(1,0)代入y=ax2+bx+c得a+b+c=0,得c=-3a;
(2)过点M作MN⊥y轴,如图1,
∵S四边形AMCO=S梯形AMNO-S△CMN,
∴S四边形AMCO=S梯形AMNO-S△CMN=$\frac{1}{2}$×4a×(3+1)-$\frac{1}{2}$×1×(4a+c)
=8a-$\frac{1}{2}$a
=$\frac{15}{2}$a,
∴S△COB=$\frac{1}{2}$×1×(-c)=$\frac{3}{2}$a,
∴$\frac{{S}_{△COB}}{{S}_{四边形AMCO}}$=$\frac{\frac{3}{2}a}{\frac{15}{2}a}$=$\frac{1}{5}$;
(3)①过点M作MH⊥x轴,如图1,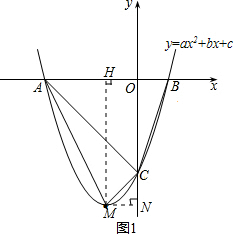
∵∠ACM=90°,
∴AM2=AC2+CM2,
∵AM2=AH2+MH2,AC2=OA2+OC2,CM2=CN2+MN2,
∴4+16a2=9+c2+1+(4a+c)2,
解得a=±1,
∵抛物线开口向上,∴a>0,
∴a=1,
∴b=2,c=-3,
∴抛物线的解析式为y=x2+2x-3,
∴点C(0,-3),M(-1,-4),H(-1,0),
∵OA=OC=3,∴∠OAC=∠OCA=45°,
∵tan∠MAC=$\frac{MC}{AC}$=$\frac{\sqrt{2}}{3\sqrt{2}}$=$\frac{1}{3}$,tan∠OCB=$\frac{OB}{OC}$=$\frac{1}{3}$,
∴∠MAC=∠OCB,
∵∠MAO=∠MAC+∠OAC,∠ACB=∠ACO+∠OCB,
∴∠MAO=∠ACB;
②假设存在点D,使以点A、O、D为顶点的三角形与△ACB相似.如图2,
设直线AM的解析式y=kx+b,
把(-3,0)(-1,-4)代入得$\left\{\begin{array}{l}{-3k+b=0}\\{-k+b=-4}\end{array}\right.$,
解得k=-2,b=-6,
∴直线AM的解析式为y=-2x-6,
∵点D在线段AM上,∴设点D坐标(m,-2m-6),
分两种情况讨论:
第一种情况△AOD∽△CAB,
∴∠AOD=∠CAB=45°,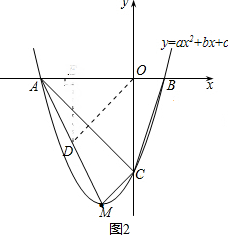
∴直线OD的解析式为y=x,
由$\left\{\begin{array}{l}{y=x}\\{y=-2x-6}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=-2}\end{array}\right.$,
∴D(-2,-2),
第二种情况△AOD∽△CBA,
∴∠AOD=∠ABC,
∴OD∥BC,
∵直线BC的解析式为y=3x-3,
∴直线OD的解析式为y=3x,
由$\left\{\begin{array}{l}{y=3x}\\{y=-2x-6}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{6}{5}}\\{y=-\frac{18}{5}}\end{array}\right.$,
∴D(-$\frac{6}{5}$,-$\frac{18}{5}$)
综上所述,点D的坐标为(-2,-2),(-$\frac{6}{5}$,-$\frac{18}{3}$).
点评 本题考查了二次函数的综合题,涉及的知识点有直角三角形的性质、二次函数解析式的确定以及相似三角形的判定和性质,要注意当相似三角形的对应边和对应角不确定的情况下需要分类讨论,以免漏解.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:填空题
 线段的垂直平分线的性质1:
线段的垂直平分线的性质1:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
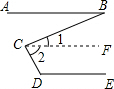 根据题意完成下列推理过程:
根据题意完成下列推理过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com