
ΓΨΧβΡΩΓΩΘ®2013ΡξΥΡ¥®Ή ―τ11Ζ÷Θ©‘Ύ“ΜΗω±Ώ≥ΛΈΣaΘ®ΒΞΈΜΘΚcmΘ©ΒΡ’ΐΖΫ–ΈABCD÷–Θ§ΒψEΓΔMΖ÷±π «œΏΕΈACΘ§CD…œΒΡΕ·ΒψΘ§Ν§ΫαDE≤Δ―”≥ΛΫΜ’ΐΖΫ–ΈΒΡ±Ώ”ΎΒψFΘ§ΙΐΒψMΉςMNΓΆDF”ΎHΘ§ΫΜAD”ΎNΘ°
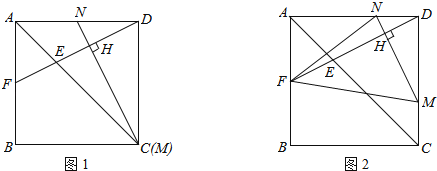
Θ®1Θ©»γΆΦ1Θ§Β±ΒψM”κΒψC÷ΊΚœΘ§«σ÷ΛΘΚDF=MNΘΜ
Θ®2Θ©»γΆΦ2Θ§ΦΌ…ηΒψM¥”ΒψC≥ωΖΔΘ§“‘1cm/sΒΡΥΌΕ»―ΊCDœρΒψD‘ΥΕ·Θ§ΒψEΆ§ ±¥”ΒψA≥ωΖΔΘ§“‘![]() cm/sΥΌΕ»―ΊACœρΒψC‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΘ®tΘΨ0Θ©ΘΜ
cm/sΥΌΕ»―ΊACœρΒψC‘ΥΕ·Θ§‘ΥΕ· ±ΦδΈΣtΘ®tΘΨ0Θ©ΘΜ
ΔΌ≈–ΕœΟϋΧβΓΑΒ±ΒψF «±ΏAB÷–Βψ ±Θ§‘ρΒψM «±ΏCDΒΡ»ΐΒ»Ζ÷ΒψΓ±ΒΡ’φΦΌΘ§≤ΔΥΒΟςάμ”…Θ°
ΔΎΝ§ΫαFMΓΔFNΘ§ΓςMNFΡήΖώΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τΡήΘ§«κ–¥≥ωaΘ§t÷°ΦδΒΡΙΊœΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®1Θ©÷ΛΟςΘΚΓΏΓœDNC+ΓœADF=90ΓψΘ§ΓœDNC+ΓœDCN=90ΓψΘ§ΓύΓœADF=ΓœDCNΓΘ
‘ΎΓςADF”κΓςDNC÷–Θ§ΓΏ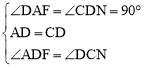 Θ§
Θ§
ΓύΓςADFΓ’ΓςDNCΘ®ASAΘ©ΓΘΓύDF=MNΓΘ
Θ®2Θ©ΔΌΗΟΟϋΧβ «’φΟϋΧβΓΘάμ”…»γœ¬ΘΚ
Β±ΒψF «±ΏAB÷–Βψ ±Θ§‘ρAF=![]() AB=
AB=![]() CDΓΘ
CDΓΘ
ΓΏABΓΈCDΘ§ΓύΓςAFEΓΉΓςCDEΘ§
Γύ![]() ΓΘΓύAE=
ΓΘΓύAE=![]() ECΘ§‘ρAE=
ECΘ§‘ρAE=![]() AC=
AC=![]() aΓΘΓύ
aΓΘΓύ![]() ΓΘ
ΓΘ
ΓύCM=1t=![]() a=
a=![]() CDΓΘ
CDΓΘ
ΓύΒψMΈΣ±ΏCDΒΡ»ΐΒ»Ζ÷Βψ
ΔΎΡήΓΘάμ”…»γœ¬ΘΚ
“Ή÷ΛAFEΓΉΓςCDEΘ§Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§ΒΟ
Θ§ΒΟ![]() ΓΘ
ΓΘ
“Ή÷ΛΓςMNDΓΉΓςDFAΘ§Γύ![]() Θ§Φ¥
Θ§Φ¥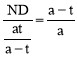 Θ§ΒΟND=tΓΘ
Θ§ΒΟND=tΓΘ
ΓύND=CM=tΘ§AN=DM=a©¹tΓΘ
»τΓςMNFΈΣΒ»―ϋ»ΐΫ«–ΈΘ§‘ρΩ…Ρή”–»ΐ÷÷«ι–ΈΘΚ
Θ®IΘ©»τFN=MNΘ§‘ρ”…AN=DM÷ΣΓςFANΓ’ΓςNDMΘ§
ΓύAF=DMΘ§Φ¥![]() =tΘ§ΒΟt=0Θ§≤ΜΚœΧβ“βΓΘΓύ¥Υ÷÷«ι–Έ≤Μ¥φ‘ΎΓΘ
=tΘ§ΒΟt=0Θ§≤ΜΚœΧβ“βΓΘΓύ¥Υ÷÷«ι–Έ≤Μ¥φ‘ΎΓΘ
Θ®IIΘ©»τFN=FMΘ§”…MNΓΆDF÷ΣΘ§HN=HMΘ§ΓύDN=DM=MCΘ§
Γύt=![]() aΘ§¥Υ ±ΒψF”κΒψB÷ΊΚœΓΘ
aΘ§¥Υ ±ΒψF”κΒψB÷ΊΚœΓΘ
Θ®IIIΘ©»τFM=MNΘ§œ‘»Μ¥Υ ±ΒψF‘ΎBC±Ώ…œΘ§»γΆΦΥυ ΨΘ§
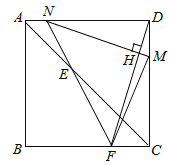
“ΉΒΟΓςMFCΓ’ΓςNMDΘ§ΓύFC=DM=a©¹tΓΘ
”÷”…ΓςNDMΓΉΓςDCFΘ§Γύ![]() Θ§Φ¥
Θ§Φ¥![]()
Γύ![]() ΓΘ
ΓΘ
Γύ![]() =a©¹tΓΘ
=a©¹tΓΘ
Γύt=aΘ§¥Υ ±ΒψF”κΒψC÷ΊΚœΓΘ
Ήέ…œΥυ ωΘ§Β±t=aΜρt=![]() a ±Θ§ΓςMNFΡήΙΜ≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΓΘ
a ±Θ§ΓςMNFΡήΙΜ≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΓΘ
ΓΨΫβΈωΓΩΘ®1Θ©÷ΛΟςΓςADFΓ’ΓςDNCΘ§Φ¥Ω…ΒΟΒΫDF=MNΓΘ
Θ®2Θ©ΔΌ Ήœ»÷ΛΟςΓςAFEΓΉΓςCDEΘ§άϊ”Ο±»άΐ Ϋ«σ≥ω ±Φδt=![]() aΘ§ΫχΕχΒΟΒΫCM=
aΘ§ΫχΕχΒΟΒΫCM=![]() a=
a=![]() CDΘ§Υυ“‘ΗΟΟϋΧβΈΣ’φΟϋΧβΓΘ
CDΘ§Υυ“‘ΗΟΟϋΧβΈΣ’φΟϋΧβΓΘ
ΔΎ»τΓςMNFΈΣΒ»―ϋ»ΐΫ«–ΈΘ§‘ρΩ…Ρή”–»ΐ÷÷«ι–ΈΘ§–η“ΣΖ÷άύΧ÷¬έΓΘ


 ’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
’ψ¥σ”≈―ß–Γ―ßΡξΦΕœΈΫ”ΫίΨΕ’ψΫ≠¥σ―ß≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςAOB÷–Θ§ABΓΆOBΘ§«“AB=OB=3Θ§…η÷±œΏ![]() ΫΊ¥Υ»ΐΫ«–ΈΥυΒΟ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§‘ρS”κt÷°ΦδΒΡΚ· ΐΙΊœΒΒΡΆΦœσΈΣœ¬Ν–―Γœν÷–ΒΡΘ®ΓΓΓΓΘ©
ΫΊ¥Υ»ΐΫ«–ΈΥυΒΟ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ§‘ρS”κt÷°ΦδΒΡΚ· ΐΙΊœΒΒΡΆΦœσΈΣœ¬Ν–―Γœν÷–ΒΡΘ®ΓΓΓΓΘ©

A.  B.
B.  C.
C.  D.
D. 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩψτœΊ‘Ύ ΓΦΕΈΡΟς≥« –¥¥Ϋ®÷–Θ§ΨΌ––ΓΑ–Γ ÷ά≠¥σ ÷Θ§≥ΪΒΦΈΡΟς–¬Ζγ…–Γ±ΒΡΜνΕ·÷–Θ§Ψ≈ΡξΦΕΒΡ5ΟϊΆ§―ßΘ®»ΐΡ–ΝΫ≈°Θ©≥…ΝΔΝΥΓΑΫΜΆ®÷»–ρΈ§ΜΛΓ±–ΓΖ÷Ε”Θ§»τ¥”ΗΟ–ΓΖ÷Ε”÷–»Έ―ΓΝΫΟϊΆ§―ßΫχ––ΫΜΆ®÷»–ρΈ§ΜΛΘ§‘ρ«Γ «“ΜΡ–“Μ≈°ΒΡΗ≈¬ «Εύ…ΌΘΩ«κ”Ο ςΉ¥ΆΦΜρΝ–±μΖ®ΥΒΟςΥυ”–Ω…ΡήΒΡΫαΙϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΖ¥”≥ΒΡΙΐ≥Χ «–ΓΟς¥”Φ“»Ξ ≥ΧΟ≥‘‘γ≤ΆΘ§Ϋ”Ή≈»ΞΆΦ ιΙίΕΝ±®Θ§»ΜΚσΜΊΦ“Θ§Τδ÷–x±μ Ψ ±ΦδΘ§y±μ Ψ–ΓΟςάκΦ“ΒΡΨύάκΘ§–ΓΟςΦ“ΓΔ ≥ΧΟΓΔΆΦ ιΙί‘ΎΆ§“Μ÷±œΏ…œΘ§ΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
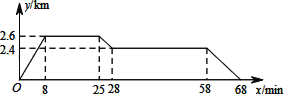
A. ≥ΧΟάκ–ΓΟςΦ“2Θ°4km
B.–ΓΟς‘ΎΆΦ ιΙί¥τΝΥ20min
C.–ΓΟς¥”ΆΦ ιΙίΜΊΦ“ΒΡΤΫΨυΥΌΕ» «0Θ°04km/min
D.ΆΦ ιΙί‘Ύ–ΓΟςΦ“ΚΆ ≥ΧΟ÷°ΦδΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Ήχ±ξœΒ÷–”–![]() Θ§
Θ§![]() ΈΣΉχ±ξ‘≠ΒψΘ§
ΈΣΉχ±ξ‘≠ΒψΘ§![]() Θ§ΫΪ¥Υ»ΐΫ«–Έ»Τ‘≠Βψ
Θ§ΫΪ¥Υ»ΐΫ«–Έ»Τ‘≠Βψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() Θ§Εΰ¥ΈΚ· ΐ
Θ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσΗ’ΚΟΨ≠Ιΐ
ΒΡΆΦœσΗ’ΚΟΨ≠Ιΐ![]() »ΐΒψΘ°
»ΐΒψΘ°
Θ®1Θ©«σΕΰ¥ΈΚ· ΐΒΡΫβΈω ΫΦΑΕΞΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®2Θ©ΙΐΕ®Βψ![]() ΒΡ÷±œΏ
ΒΡ÷±œΏ![]() ”κΕΰ¥ΈΚ· ΐΆΦœσœύΫΜ”Ύ
”κΕΰ¥ΈΚ· ΐΆΦœσœύΫΜ”Ύ![]() ΝΫΒψΘ°
ΝΫΒψΘ°
ΔΌ»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
ΔΎ÷ΛΟςΘΚΈό¬έ![]() ΈΣΚΈ÷ΒΘ§
ΈΣΚΈ÷ΒΘ§![]() ΚψΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
ΚψΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
ΔέΒ±÷±œΏ![]() »ΤΉ≈Ε®Βψ
»ΤΉ≈Ε®Βψ![]() –ΐΉΣ ±Θ§
–ΐΉΣ ±Θ§![]() ΆβΫ”‘≤‘≤–Ρ‘Ύ“ΜΧθ≈ΉΈοœΏ…œ‘ΥΕ·Θ§÷±Ϋ”–¥≥ωΗΟ≈ΉΈοœΏΒΡ±μ¥ο ΫΘ°
ΆβΫ”‘≤‘≤–Ρ‘Ύ“ΜΧθ≈ΉΈοœΏ…œ‘ΥΕ·Θ§÷±Ϋ”–¥≥ωΗΟ≈ΉΈοœΏΒΡ±μ¥ο ΫΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣ ”Π–¬÷–ΩΦ”Δ”οΧΐΥΒΜζΩΦΘ§Ψ≈ΡξΦΕΦΉΓΔ““ΝΫΈΜΆ§―ß Ι”ΟΡ≥ ÷Μζ»μΦΰΫχ––”Δ”οΧΐΥΒΝΖœΑ≤ΔΦ«¬ΦΝΥ40¥ΈΒΡΝΖœΑ≥…Φ®Θ°ΦΉΓΔ““ΝΫΈΜΆ§―ßΒΡΝΖœΑ≥…Φ®Ά≥ΦΤΫαΙϊ»γΆΦΥυ ΨΘΚ

œ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
A. ΦΉΆ§―ßΒΡΝΖœΑ≥…Φ®ΒΡ÷–ΈΜ ΐ «38Ζ÷
B. ““Ά§―ßΒΡΝΖœΑ≥…Φ®ΒΡ÷Ύ ΐ «15Ζ÷
C. ΦΉΆ§―ßΒΡΝΖœΑ≥…Φ®±»““Ά§―ßΒΡΝΖœΑ≥…Φ®ΗϋΈ»Ε®
D. ΦΉΆ§―ßΒΡΝΖœΑΉή≥…Φ®±»““Ά§―ßΒΡΝΖœΑΉή≥…Φ®ΒΆ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
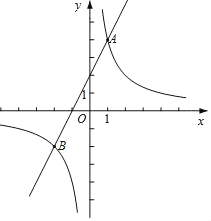
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§÷±œΏyΘΫ2x+2”κΚ· ΐyΘΫ![]() Θ®kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§«“ΒψAΒΡΉχ±ξΈΣΘ®1Θ§mΘ©Θ°
Θ®kΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ§BΝΫΒψΘ§«“ΒψAΒΡΉχ±ξΈΣΘ®1Θ§mΘ©Θ°
Θ®1Θ©«σkΘ§mΒΡ÷ΒΘΜ
Θ®2Θ©“―÷ΣΒψPΘ®aΘ§0Θ©Θ§ΙΐΒψPΉςΤΫ––”Ύy÷αΒΡ÷±œΏΘ§ΫΜ÷±œΏyΘΫ2x+2”ΎΒψMΘ§ΫΜΚ· ΐyΘΫ![]() Θ®kΓΌΘ©ΒΡΆΦœσ”ΎΒψNΘ°
Θ®kΓΌΘ©ΒΡΆΦœσ”ΎΒψNΘ°
ΔΌΒ±aΘΫ2 ±Θ§«σœΏΕΈMNΒΡ≥ΛΘΜ
ΔΎ»τPMΘΨPNΘ§ΫαΚœΚ· ΐΒΡΆΦœσΘ§÷±Ϋ”–¥≥ωaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
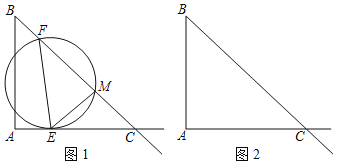
ΓΨΧβΡΩΓΩ»γΆΦΘ§RtΓςABC÷–Θ§ABΘΫ6Θ§ACΘΫ8Θ°Ε·ΒψEΘ§FΆ§ ±Ζ÷±π¥”ΒψAΘ§B≥ωΖΔΘ§Ζ÷±π―ΊΉ≈…δœΏACΚΆ…δœΏBCΒΡΖΫœρΨυ“‘ΟΩΟκ1ΗωΒΞΈΜΒΡΥΌΕ»‘ΥΕ·Θ§Ν§Ϋ”EFΘ§“‘EFΈΣ÷±ΨΕΉςΓ―OΫΜ…δœΏBC”ΎΒψMΘ§Ν§Ϋ”EMΘ§…η‘ΥΕ·ΒΡ ±ΦδΈΣtΘ®tΘΨ0Θ©Θ°
Θ®1Θ©Β±ΒψE‘ΎœΏΕΈAC…œ ±Θ§”ΟΙΊ”ΎtΒΡ¥ζ ΐ Ϋ±μ ΨCEΘΫΓΓ ΓΓΘ§CMΘΫΓΓ ΓΓΘ°Θ®÷±Ϋ”–¥≥ωΫαΙϊΘ©
Θ®2Θ©‘Ύ’ϊΗω‘ΥΕ·Ιΐ≥Χ÷–Θ§Β±tΈΣΚΈ÷Β ±Θ§“‘ΒψEΓΔFΓΔMΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ“‘ΒψAΓΔBΓΔCΈΣΕΞΒψΒΡ»ΐΫ«–ΈœύΥΤΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
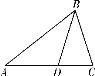
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§BD «ΓςABCΒΡΫ«ΤΫΖ÷œΏΘ°
(1)≥ΏΙφΉςΆΦΘΚΉςBDΒΡ¥Ι÷±ΤΫΖ÷œΏΖ÷±πΫΜABΘ§BC”ΎΒψMΘ§NΘΜ(±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ–¥ΉςΖ®)
(2)Ν§Ϋ”MDΘ§NDΘ§≈–ΕœΥΡ±Ώ–ΈBMDNΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com