
����Ŀ��ͼ�����۵������л��γ���ȵıߺ���ȵĽǣ�������ͬѧ������ѧ���������������Ρ��ı����۵�ʵ�飬�����ʵ����̽�����⣺ 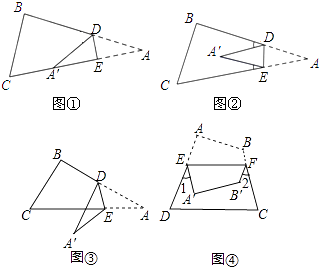
���⣨һ��
��ͼ�٣�һ��������ABCֽƬ����D��E�ֱ��ǡ�ABC�������㣮
��1�������ֱ��DE�۵���ʹA������CE�ϣ����BDA��͡�A��������ϵ����
��2������۳�ͼ�ڵ���״�������BDA�䡢��CEA��͡�A��������ϵ����
��3������۳�ͼ�۵���״�������BDA�䡢��CEA��͡�A��������ϵ����˵�����ɣ�
��4����ͼ�ܣ����ı���ABCDֽƬ��EF�۵���ʹ��A��B�����ı���EFCD���ڲ�ʱ����1+��2���A����B֮���������ϵ�� �� ��ֱ��д�����ۣ�
���𰸡�
��1����BDA=2��A
��2����BDA��+��CEA��=2��A
��3���⣺��BDA�䩁��CEA��=2��A��
֤�����£�
����AA�乹����������Σ�
��BDA��=2��DA'A����CEA'=2��EA'A��
�á�BDA'����CEA'=2��A
��4����1+��2=2����A+��B����360��
���������⣺��1.���߸����۵������ʿ�֪��DA��E=��A����DA��E+��A=��BDA�䣬����BDA=2��A��
���Դ��ǣ���BDA=2��A��
��2.����ͼ���۵������ʿ�֪����CEA��=180�㩁2��DEA�䡭�٣���BDA��=180�㩁2��A��DE���ڣ�
��+�ڵã���BDA��+��CEA��=360�㩁2����DEA��+��A��DE
����BDA��+��CEA��=360�㩁2��180�㩁��A����
�ʡ�BDA��+��CEA��=2��A��
���Դ��ǣ���BDA��+��CEA��=2��A��
��4.����ͼ�ܣ���ͼ���۵������ʿ�֪��1=180�㩁2��AEF����2=180�㩁2��BFE��
��ʽ��ӵã���1+��2=360�㩁2����AEF+��BFE��
����1+��2=360�㩁2��360�㩁��A����B����
���ԣ���1+��2=2����A+��B����360�㣮
���Դ��ǣ���1+��2=2����A+��B����360�㣮
�����㾫�����������⣬������Ҫ�˽�ƽ���ߵ�����(��ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ���)����Ҫ���������ε��ڽǺ����(�����ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽ�)�����֪ʶ���Ǵ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��B��E��F��C������ͬһ��ֱ���ϣ�AF��BC��DE��BC������ֱ�ΪF��E����AB=DC��BE=CF����˵��AB��DC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2+mx��6=0��һ����Ϊ2����m��ֵ����һ�����ǣ� ��
A.1��3
B.��1��3
C.1����3
D.��1����3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCֽƬ��һ���۵���ʹ��C���ڡ�ABC��һ��C���ϣ�����1=30�㣬��2=36�㣬���C�Ķ����ǣ� ��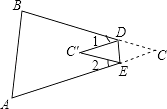
A.33��
B.34��
C.31��
D.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ԭ����Ϊn�֣�����30%��IJ���Ϊ�� ��
A.30%n��
B.��1��30%��n��
C.��1+30%��n��
D.��n+30%����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com