
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
①求证:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:

下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A( ![]() ,0)、B(3
,0)、B(3 ![]() ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A.2 ![]() ﹣2
﹣2
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2018秒时,点P的坐标是( )
个单位长度,则第2018秒时,点P的坐标是( )
![]()
A. (2016,0) B. (2017,0) C. (2018,0) D. (2017,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两根直杆隔河相对,杆CD高30m,杆AB高20m,两杆相距50m.现两杆上各有一只鱼鹰,它们同时看到两杆之间的河面上E处浮起一条小鱼,于是以同样的速度同时飞下来夺鱼,结果两只鱼鹰同时到达,叼住小鱼.问两杆底部距鱼的距离各是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每个每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是( )
A. 3分钟 B. 3.75分钟 C. 4分钟 D. 5分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD,BC分别切⊙O于A,B两点,CD切⊙O于点E,连接OD,OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2 , ④OD:OC=DE:EC,⑤OD2=DECD,正确的有( ) 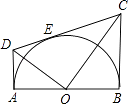
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com