
【题目】如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.

【答案】详见解析.
【解析】分析:(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF≌△DAF,得出对应边相等即可;
(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE=90°即可.
详解:证明:如图所示:

(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,
在△BAF和△DAF中,
 ,
,
∴△BAF≌△DAF(SAS),
∴BF=DF;
(2)∵BE的垂直平分线FG交对角AC于点F,
∴BF=EF,
∵BF=DF,
∴EF=DF,
∴∠FDE=∠FED,
∵△BAF≌△DAF,
∴∠ABF=∠FDE,
∴∠ABF=∠FED,
∵∠FED+∠FEA=180°,
∴∠ABF+∠FEA=180°,
∴∠BAE+∠BFE=180°,
∴∠BFE=90°,
∴BF⊥FE.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)3x+2(x2-y)-3(2x2+x-![]() y),其中x=
y),其中x=![]() ,y=-3;
,y=-3;
(2)3a2c-[2ab2-2(abc-![]() ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=-![]() ,b=2,c=3.
,b=2,c=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从![]() 地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:
地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:![]() )
)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
![]() 求收工时,检修小组在
求收工时,检修小组在![]() 地的哪个方向?距离
地的哪个方向?距离![]() 地多远?
地多远?
![]() 在第几次纪录时距
在第几次纪录时距![]() 地最远?
地最远?
![]() 若汽车行驶每千米耗油
若汽车行驶每千米耗油![]() 升,问从
升,问从![]() 地出发,检修结束后再回到
地出发,检修结束后再回到![]() 地共耗油多少升?
地共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程 | 甲类收费(元) | 乙类收费(元) |
3千米以下(包含3千米) | 7.00 | 6.00 |
3千米以上,每增加1千米 | 1.60 | 1.40 |
(1)设出租车行驶的里程为x千米(![]() 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10). 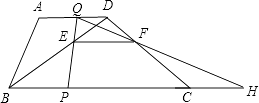
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品用了160元.
(1)求A,B两种商品每件各是多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次知识竞赛共有20道题,每一题答对得5分,答错或不答都扣3分.
(1)小明考了68分,那么小明答对了多少问题?
(2)小亮获得二等奖(70分~90分),请你算算小亮答对了几道题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com