
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E,BC=3,CD=3![]()
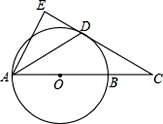
(1)求证:直线CE是⊙O的切线;
(2)求⊙O的半径;
(3)求弦AD的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连结OD,如图,由AD平分∠EAC得到∠1=∠3,加上∠1=∠2,则∠3=∠2,于是可判断OD∥AE,根据平行线的性质得OD⊥CE,然后根据切线的判定定理得到结论;
(2)连接BD.根据相似三角形的判定和性质定理即可得到结论;
(3)设BD=![]() ,AD=2k,根据勾股定理即可得到结论.
,AD=2k,根据勾股定理即可得到结论.
(1)证明:连接OD,如图,
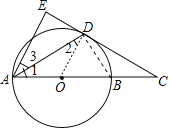
∵AD平分∠EAC,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠3=∠2,
∴OD∥AE,
∵AE⊥DC,
∴OD⊥CE,
∴CE是⊙O的切线;
(2)连接BD.
∵∠CDO=∠ADB=90°,
∴∠2=∠CDB=∠1,
∵∠C=∠C,
∴△CDB∽△CAD,
∴![]() ,
,
∴CD2=CBCA,
∴(3![]() )2=3CA,
)2=3CA,
∴CA=6,
∴AB=CA-BC=3,
∴⊙O的半径=![]() ;
;
(3)∵![]() ,设BD=
,设BD=![]() ,AD=2k,
,AD=2k,
在Rt△ADB中,2k2+4k2=9,
∴k=![]() ,
,
∴AD=![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
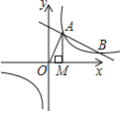
(1)求反比例函数的解析式;并直接写出不等式![]() 的解集.
的解集.
(2)在x轴上求一点P,使|PA﹣PB|的值最大,并求出其最大值和P点坐标.
(3)连接OB,求三角形AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点 M 满足横、纵坐标都为整数,则把点 M 叫做“整点”.例如:P(1,0)、Q(2,-2)都是“整点”.抛物线 y=mx2-2mx+m-1(m>0)与 x 轴交于 A、 B 两点,若该抛物线在 A、B 之间的部分与线段 AB 所围成的区域(包括边界)恰有 6 个整点,则 m 的取值范围是( )
A.![]() m
m ![]() B.
B.![]() m
m ![]() C.
C.![]() m
m ![]() D.
D.![]() m
m ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.

(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC、BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=3,则下列结论:①![]() ;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
;②S△BCE=30;③S△ABE=9;④△AEF∽△ACD,其中一定正确的是( )
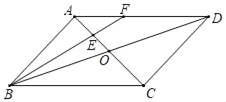
A.①②③④B.①③C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “明天降雨的概率是50%”表示明天有半天都在降雨
B. 数据4,3,5,5,0的中位数和众数都是5
C. 要了解一批钢化玻璃的最少允许碎片数,应采用普查的方式
D. 若甲、乙两组数中各有20个数据,平均数![]() =10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
=10,方差s2甲=1.25,s2乙=0.96,则说明乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
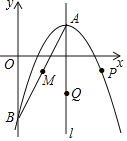
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
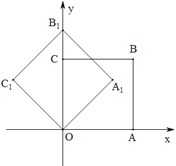
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形![]() ,依此方式,绕点O连续旋转2018次得到正方形
,依此方式,绕点O连续旋转2018次得到正方形![]() ,如果点A的坐标为(1,0),那么点
,如果点A的坐标为(1,0),那么点![]() 的坐标是______.
的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆0的直径AB垂直于弦CD于点E,CG是圆O的切线交AB的延长线于点G,连接CO并延长交AD于点F,且CF![]() AD.
AD.
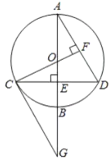
(1)试问:CG//AD吗?说明理由:
(2)证明:点E为OB的中点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com