练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】设是边长为的正三角形内的一点，到三边的距离分别为．若以为边可以组成三角形，则应满足的条件为（）

    A.B.C.D.

    【答案】B

    【解析】

    连接AP，BP，CP，先求出等边三角形的高h,然后再利用S△ABC=S△APC+S△APB+S△BPC，再找出x，y，z与h的关系，最后运用三角形三边关系即可解答．

    解：设等边三角形的高h

    ∵等边三角形的边长为a

    ∴该等边三角形的高h=

    如图:连接AP、BP、CP，设PE=x，PF=y，PQ=z

    ∵S△ABC=S△APC+S△APB+S△BPC，

    ∴

    又∵△ABC为等边三角形，

    ∴AB=BC=AC，

    ∴，即x+y+z=h，

    ∵以x，y，z为边可以组成三角形

    ∴x+y>z，

    ∴2z＜h，即z＜

    又∵x≤y≤z，

    ∴z≥

    ∴

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

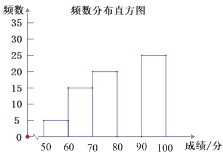
    【题目】为引领学生感受诗词之美，某校团委组织了一次全校800名学生参加的“中国诗词大赛”，赛后发现有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中100名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

    成绩x/分

    频数

    频率

    50≤x＜60

    5

    0.05

    60≤x＜70

    15

    0.15

    70≤x＜80

    20

    n

    80≤x＜90

    m

    0.35

    90≤x≤100

    25

    0.25

    请根据所给信息，解答下列问题：

    （1）m= ，n= ；并补全频数分布直方图；

    （2）这100名学生成绩的中位数会落在分数段；

    （3）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的800名学生中成绩“优”等的约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了推动全社会自觉尊法学法守法用法，促进全面依法治国，某区每年都举办普法知识竞赛，该区某单位甲、乙两个部门各有员工200人，要在这两个部门中挑选一个部门代表单位参加今年的竞赛，为了解这两个部门员工对法律知识的掌握情况，进行了抽样调查，从甲、乙两个部门各随机抽取20名员工，进行了法律知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行整理，描述和分析，下面给出了部分信息．

    a．甲部门成绩的频数分布直方图如下（数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）

    b．乙部门成绩如下：

    40 52 70 70 71 73 77 78 80 81

    82 82 82 82 83 83 83 86 91 94

    c．甲、乙两部门成绩的平均数、方差、中位数如下：

    平均数

    方差

    中位数

    甲

    79.6

    36.84

    78.5

    乙

    77

    147.2

    m

    d．近五年该单位参赛员工进入复赛的出线成绩如下：

    2014年

    2015年

    2016年

    2017年

    2018年

    出线成绩（百分制）

    79

    81

    80

    81

    82

    根据以上信息，回答下列问题：

    （1）写出表中m的值；

    （2）可以推断出选择　 　部门参赛更好，理由为　 　；

    （3）预估（2）中部门今年参赛进入复赛的人数为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校举办学生综合素质大赛，分“单人项目”和“双人项目”两种形式，比赛题目包括下列五类：．人文艺术；．历史社会；．自然科学；．天文地理；．体育健康．

    （1）若小明参加“单人项目”，他从中抽取一个题目，那么恰好抽中“自然科学”类题目的概率为_____．

    （2）小林和小丽参加“双人项目”，比赛规定：同一小组的两名同学的题目类型不能相同，且每人只能抽取一次，求他们抽到“天文地理”和“体育健康”类题目的概率是多少？（用画树状图或列表的方法求解）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“切实减轻学生课业负担”是我市作业改革的一项重要举措．某中学为了了解本校学生平均每天的课外作业时间，随机抽取部分学生进行问卷调查，并将调查结果分为A，B，C，D四个等级，A：1小时以内；B：1小时～1.5小时；C：1.5小时～2小时；D：2小时以上(各边界值忽略不计)．根据调查结果绘制了如图所示的两幅不完整的统计图，请根据图中信息解答下列问题：

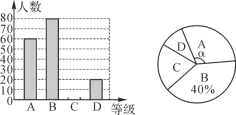
    (1)该校共调查了 　 名学生；

    (2)请将条形统计图补充完整；

    (3)表示等级A的扇形圆心角的度数是 　 ；

    (4)若该学校在校学生人数共2000人，问做课外作业时间在1.5小时～2小时的学生人数大约有多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是二次函数图象的一部分，对称轴为，且经过点，有下列说法：①；②；③；④若是抛物线上的两点，则，上述说法正确的是（ ）

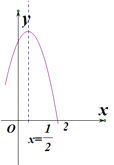
    A.①②④B.③④C.①③④D.①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一名在校大学生利用“互联网+”自主创业，销售一种产品，这种产品的成本价10元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元/件，市场调查发现，该产品每天的销售量（件与销售价（元/件）之间的函数关系如图所示．

    （1）求与之间的函数关系式，并写出自变量的取值范围；

    （2）求每天的销售利润W（元与销售价（元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，点是的中点，以为直角边向外作等腰，连接，当取最大值时，则的度数是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC=90°, ②OC=OE， ③tan∠OCD =，④中，正确的有（ ）

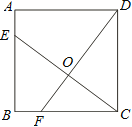
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    同步练习册答案