
23.(本题满分10分)如图,在菱形ABCD中,AB=2,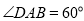 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
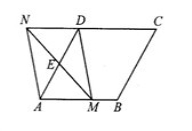
(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形.
(1)证明见解析;(2)①1;②2.
【解析】
试题分析:(1)利用菱形的性质和已知条件可证明四边形AMDN的对边平行且相等即可;
(2)①由(1)可知四边形AMDN是平行四边形,利用有一个角为直角的平行四边形为矩形,即 =90°,所以AM=
=90°,所以AM=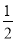 AD=1时即可;
AD=1时即可;
②当平行四边形AMDN的邻边AM=DM时,四边形为菱形,利用已知条件再证明△ADM是等边三角形即可.
试题解析:(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴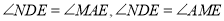 ,
,
又∵点E是AD中点,∴DE=AE,
∴ ,
,
∴四边形AMDN是平行四边形.
(2)①当AM的值为1时,四边形AMDN是矩形.理由如下:
因为AM=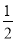 AD=1,
AD=1,
所以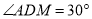 ,
,
因为 ,
,
所以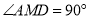 ,
,
所以平行四边形AMDN是矩形;
故答案为:1;
②当AM的值为2时,四边形AMDN是菱形.理由如下:
因为AM=2,
所以AM=AD=2,
所以△AMD是等边三角形,
所以AM=DM,
所以平行四边形AMDN是菱形.
故答案为:2.
考点:菱形的性质;矩形的判定;菱形的判定,平行四边形的判定.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
一次函数y=ax+b的图象与反比例函数 的图象交于A,B两点,与
的图象交于A,B两点,与 轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
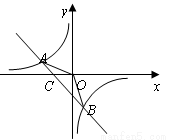
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积。
(3)根据图象写出使一次函数的值小于反比例函数的值的 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
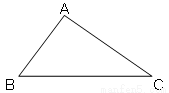
如图, 中,AC﹦5,
中,AC﹦5,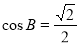 ,
, ,则
,则 的面积为( )
的面积为( )
A.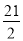 B.12 C. 14 D.21
B.12 C. 14 D.21
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分12分)在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.

(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
已知实数x、y满足 x2+2x+y-1=0,则x+2y的最大值为 .
x2+2x+y-1=0,则x+2y的最大值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
据统计,截至2014年底,全国的共产党员人数已超过80 300 000,这个数据用科学计数法可表示为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题8分)如图,四边形ABCD是矩形,直线l垂直平分线段AC,垂足为O,直线l分别与线段AD、CB的延长线交于点E、F.
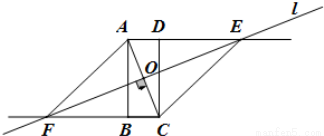
(1)△ABC与△FOA相似吗?为什么?
(2)试判定四边形AFCE的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com