【题目】如图，点P关于OA、OB的对称点分别为H、G，直线HG交OA、OB于点C、D，若∠HOG=80°，则∠CPD=___________．
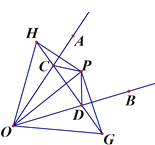
【答案】100°
【解析】
要求∠CPD的度数，要在△CPD中进行，根据轴对称的性质和等腰三角形的性质找出与∠CPD的关系，利用已知可得∠AOB=40°可求出∠CPD．
解：连接OP
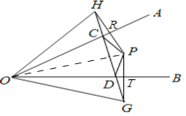
∵P关于OA、OB的对称点是H、G，
∴OA垂直平分PH于R，OB垂直平分PG于T，
∴CP=CH，DG=DP，
∴∠PCD=2∠CHP，∠PDC=2∠DGP，
∵∠PRC=∠PTD=90°，
∴在四边形OTPR中，
∴∠RPT+∠AOB=180°，
∵∠POC=∠COH，∠POD=∠DOG，∠HOG=80°，
∴∠AOB=40°
∴∠RPT=180°-40°=140°
∴∠CHP+∠PGD=40°，
∴∠PCD+∠PDC=80°
∴∠CPD=180°-80°=100°．
故答案为100°．
名校课堂系列答案科目：初中数学 来源： 题型：
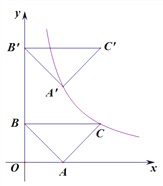
【题目】如图，在平面直角坐标系中，等腰直角三角形ABC的直角顶点在x轴上，顶点B在y轴上，顶点C在函数
（x＞0）的图象上，且BC∥x轴．将△ABC沿y轴正方向平移，使点A的对应点
落在此函数的图象上，则平移的距离为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：如果一个数的平方等于
，记为记
，这个数
叫做虚数单位，那么形如
(
为实数)的数就叫做复数，
叫这个复数的实部，
叫做这个复数的虚部。它有如下特点：①它的加，减，乘法运算与整式的加，减，乘法运算类似。例如计算：
；
②若他们的实部和虚部分别相等，则称这两个复数相等；若它们的实部相等，虚部互为相反数，则称这两个复数共轭，如
的共轭复数为
。
（1）填空：
；
。
（2）求
的共轭复数：
（3）已知
，其中
为正整数，求
的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，A、B为x轴上两点，C、D为y轴上的两点，经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封
闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线C2：
（
＜0）的顶点．
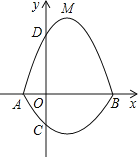
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】近几年，随着电子商务的快速发展，“电商包裹件”占“快递件”总量的比例逐年增长，根据企业财报，某网站得到如下统计表：
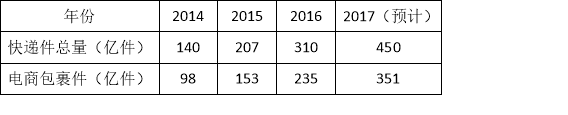
（1）请选择适当的统计图，描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比（精确到1%）；
（2）若2018年“快递件”总量将达到675亿件，请估计其中“电商包裹件”约为多少亿件？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知数轴上点A表示的数为﹣1，点B表示的数为3，点P为数轴上一动点．
（1）点A到原点O的距离为 个单位长度；点B到原点O的距离为 个单位长度；线段AB的长度为 个单位长度；
（2）若点P到点A、点B的距离相等，则点P表示的数为 ；
（3）数轴上是否存在点P，使得PA+PB的和为6个单位长度？若存在，请求出PA的长；若不存在，请说明理由？
（4）点P从点A出发，以每分钟1个单位长度的速度向左运动，同时点Q从点B出发，以每分钟2个单位长度的速度向左运动，请直接回答：几分钟后点P与点Q重合？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：在数轴上
点表示数
，
点表示数6，
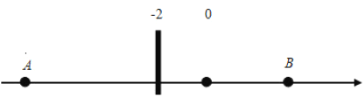
（1）A、B两点之间的距离等于_________；
（2）在数轴上有一个动点
，它表示的数是
，则
的最小值是_________；
（3）若点与点
之间的距离表示为
，点与点之间的距离表示为
，请在数轴上找一点，使
，则点表示的数是_________；
（4）若在原点
的左边2个单位处放一挡板，一小球甲从点处以5个单位/秒的速度向右运动；同时另一小球乙从点处以2个单位/秒的速度向左运动，在碰到挡板后（忽略球的大小，可看作一点）两球分别以原来的速度向相反的方向运动，设运动时间为
秒，请用来表示甲、乙两小球之间的距离
.
查看答案和解析>>
科目：初中数学 来源： 题型：
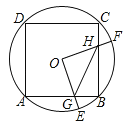
【题目】（2016湖北省咸宁市）如图，边长为4的正方形ABCD内接于点O，点E是
上的一动点（不与A、B重合），点F是
上的一点，连接OE、OF，分别与AB、BC交于点G，H，且∠EOF=90°，有以下结论：
①
；
②△OGH是等腰三角形；
③四边形OGBH的面积随着点E位置的变化而变化；
④△GBH周长的最小值为
．
其中正确的是________（把你认为正确结论的序号都填上）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若抛物线L：y=ax2+bx+c（a，b，c是常数，abc≠0）与直线l都经过y轴上的同一点，且抛物线L的顶点在直线l上，则称次抛物线L与直线l具有“一带一路”关系，并且将直线l叫做抛物线L的“路线”，抛物线L叫做直线l的“带线”．
（1）若“路线”l的表达式为y=2x﹣4，它的“带线”L的顶点的横坐标为﹣1，求“带线”L的表达式；
（2）如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系，求m，n的值；
（3）设（2）中的“带线”L与它的“路线”l在y轴上的交点为A．已知点P为“带线”L上的点，当以点P为圆心的圆与“路线”l相切于点A时，求出点P的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com