
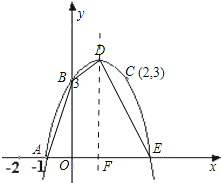
【题目】已知:如图,抛物线c1经过A,B,C三点,顶点为D,且与x轴的另一个交点为E.
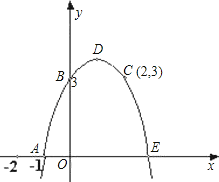
(1)求抛物线c1解析式;
(2)求四边形ABDE的面积;
(3)△AOB与△BDE是否相似,如果相似,请予以证明;如果不相似,请说明理由;
(4)设抛物线c1的对称轴与x轴交于点F,另一条抛物线c2经过点E(抛物线c2与抛物线c1不重合),且顶点为M(a,b),对称轴与x轴相交于点G,且以M,G,E为顶点的三角形与以D,E,F为顶点的三角形全等,求a,b的值.(只需写出结果,不必写出解答过程)
【答案】(1)y=﹣x2+2x+3;(2)S四边形ABDE=9(平方单位);(3)见解析;(4)![]() ,
, ,
,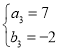 ,
,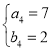 ,
,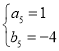 ,
,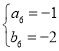 ,
,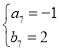 .
.
【解析】
(1)根据图象可得出A、B、C三点的坐标,然后用待定系数法即可求出抛物线的解析式;(2)由于四边形ABDE不是规则的四边形,因此可过D作DF⊥x轴于F,将四边形ABDE分成△AOB,梯形BOFD和△DFE三部分来求;(3)可先根据坐标系中两点间的距离公式,分别求出AB、BE、DE、BD的长,然后看两三角形的线段是否对应成比例即可;(4)要使两三角形全等,那么两直角三角形的两直角边应对应相等.
当EF=EG=2,DF=MG=4,此时M点的坐标可能为(5,4),(5,﹣4),(1,﹣4).
当EF=MG=2,DF=EG=4,此时M点的坐标可能是(7,2),(7,﹣2),(﹣1,2),(﹣1,﹣2);综上所述可得出a、b的值.
(1)设c1的解析式为y=ax2+bx+c,由图象可知:c1过A(﹣1,0),B(0,3),C(2,3)三点.
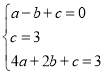 ,
,
解得: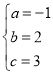 ,
,
∴抛物线c1的解析式为y=﹣x2+2x+3,
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4.
∴抛物线![]() 的顶点D的坐标为(1,4);
的顶点D的坐标为(1,4);
过D作DF⊥x轴于F,由图象可知:OA=1,OB=3,OF=1,DF=4;
令y=0,则﹣x2+2x+3=0,
解得x1=﹣1,x2=3
∴OE=3,则FE=2.
S△ABO=![]() OAOB=
OAOB=![]() ×1×3=
×1×3=![]() ;
;
S△DFE=![]() DFFE=
DFFE=![]() ×4×2=4;
×4×2=4;
S梯形BOFD=![]() (BO+DF)OF=
(BO+DF)OF=![]() ;
;
∴S四边形ABDE=S△AOB+S梯形BOFD+S△DFE=9(平方单位).
(3)如图,过B作BK⊥DF于K,则BK=OF=1.
DK=DF﹣OB=4﹣3=1.
∴BD=![]() ,
,
又DE=![]() ;
;
AB=![]() ,BE=3
,BE=3![]() ;
;
在△ABO和△BDE中,
AO=1,BO=3,AB=![]() ,
,
BD=![]() ,BE=3
,BE=3![]() , DE=2
, DE=2![]() ,
,
∵![]() ,
,
∴△AOB∽△DBE.
(4)令y=0,则![]()
解得![]()
∴点E的坐标为(3, 0),
由(1)可知物线![]() 的顶点D的坐标为(1,4)
的顶点D的坐标为(1,4)
∴F的坐标为(1,0),
∴DF=4,EF=3-1=2,
∵以M、G. E为顶点的三角形与以D、E. F为顶点的三角形全等,
∵M(a,b),
∴G,(a,0)
∴![]()
EG与DF是对应边时,EG=DF=4, MG=EF=2,
∴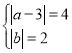
解得![]() 或
或![]()
∴![]() 或
或![]() 或
或 ![]() 或
或![]() .
.
EG与EF是对应边时,EG=EF=2, MG=DF=4,
∴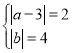
解得![]() 或
或![]()
∴![]() 或
或![]() 或
或![]() 或
或![]() (舍去),
(舍去),
综上所述:![]() ,
,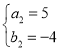 ,
,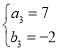 ,
,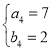 ,
,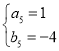 ,
,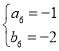 ,
,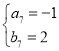 .
.
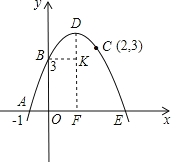


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
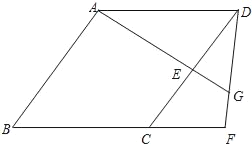
【题目】已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.
(1)求证:∠CDF=∠DAE;
(2)如果DE=CE,求证:AE=3EG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象过点(1,![]() )、(2,4)、(﹣1,
)、(2,4)、(﹣1,![]() )与x轴分别交于B(左)、C两点,与y轴交于点A.
)与x轴分别交于B(左)、C两点,与y轴交于点A.
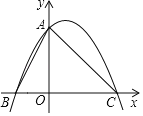
(1)求二次函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)直接写出BC的长是 ,点D的坐标是 ;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年重庆旅游近几年来非常火热,重庆作为国内最引人注目的“网红城市”,在国庆节期间接待游客数量高达3859万人数,远远抛离了第二名武汉,超越其1000多万游客,国庆期间某外地旅行团来重庆的网红景点打卡游览结束后旅行社对该旅行团做了一次“我最喜爱的巴渝景点”问卷调查(每名游客都填了调查表,且只选了一个景点),统计后发现洪崖洞、长江索道、李子坝轻轨站、磁器口榜上有名.其中选李子坝轻轨站的人数比进磁器口的少8人;选洪崖洞的人数不仅比磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的5倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,过点B作BE⊥CD,垂足为E,连接AE.F为AE上一点,且∠BFE=∠C.

(1)试说明:△ABF∽△EAD;
(2)若AB=8,BE=6,AD=9,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com