
【题目】如图所示:
![]()
(1)折叠数轴,若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)折叠数轴,若-1表示的点与5表示的点重合,则4表示的点与 表示的点重合;
(3)已知数轴上点A表示的数是-1,点B表示的数是2,若点A以每秒1个单位长度的速度在数轴上移动,点B以每秒2个单位长度的速度在数轴上移动,且点A始终在点B的左侧,求经过几秒时,A、B两点的距离为6个单位长度.
【答案】(1)2;(2)0;(3)1秒或3秒
【解析】
(1)根据题意得出-2对应的点即可;
(2)根据-1与5重合,得到2为对称轴,求出4对应的点即可;
(3)根据题意,分点A向左运动、点B向右运动,点A、点B都向右运动两种情况讨论即可得.
(1)根据题意得:原点为对称轴,即-2对应的点为2,
故答案为:2;
(2)根据题意得:2为对称轴,则表示4的点与表示0的点重合,
故答案为:0;
(3)因为点A表示的数是-1,点B表示的数是2,所以A、B两点的距离是3个单位长度,
因为点A 始终在点B的左侧,
所以当点A和点B都向右同时移动时(6-3)÷(2-1)=3(秒),
当点A向左、点B向右同时移动时(6-3)÷(1+2)=1(秒),
答:经过1秒或3秒时,A、B两点的距离为6个单位长度.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
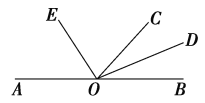
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.
(1)OD与OE的位置关系是______;(2)∠EOC的余角是_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)3x+2(x2-y)-3(2x2+x-![]() y),其中x=
y),其中x=![]() ,y=-3;
,y=-3;
(2)3a2c-[2ab2-2(abc-![]() ab2)+3a2c]-abc,其中a=-
ab2)+3a2c]-abc,其中a=-![]() ,b=2,c=3.
,b=2,c=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )

A. 5 B. 8 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
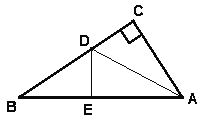
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?若能,请给出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10). 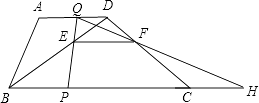
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com