
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC= ![]() ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F. 
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC= ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:连接AF.
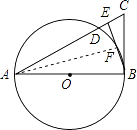
∵AB为直径,
∴∠AFB=90°.
∵AE=AB,
∴△ABE为等腰三角形.
∴∠BAF= ![]() ∠BAC.
∠BAC.
∵∠EBC= ![]() ∠BAC,
∠BAC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.
即AB⊥BC,
∴BC与⊙O相切
(2)解:过E作EG⊥BC于点G,
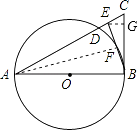
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC= ![]() .
.
在△AFB中,∠AFB=90°,
∵AB=8,
∴BF=ABsin∠BAF=8× ![]() =2,
=2,
∴BE=2BF=4.
在△EGB中,∠EGB=90°,
∴EG=BEsin∠EBC=4× ![]() =1,
=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴ ![]() .
.
∴ ![]() ,
,
∴CE= ![]() ,
,
∴AC=AE+CE=8+ ![]() =
= ![]() .
.
【解析】(1)首先连接AF,由AB为直径,根据圆周角定理,可得∠AFB=90°,又由AE=AB,∠EBC= ![]() ∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B. 
(1)求证:∠AEF=∠BCE;
(2)当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;
(3)探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1). 
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的位似比为1:2,画出△A1B2C2(△ABC与△A1B2C2在位似中心O点的两侧,A,B,C的对应点分别是A1 , B2 , C2).
(2)利用方格纸标出△A1B2C2外接圆的圆心P,P点坐标是 , ⊙P的半径= . (保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2的度数为( ) 
A.120°
B.180°
C.240°
D.300°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38, ![]() ≈1.73,精确到个位)
≈1.73,精确到个位) 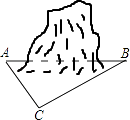
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
(1)求这条抛物线的表达式;
(2)连接AB,BD,DA,试判断△ABD的形状;
(3)点P是BD上方抛物线上的动点,当P运动到什么位置时,△BPD的面积最大?求出此时点P的坐标及△BPD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的顶点A、C在双曲线y1= ![]() 上,B、D在双曲线y2=
上,B、D在双曲线y2= ![]() 上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
上,k1=2k2(k1>0),AB//y轴,S□ABCD=24,则k1=.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+1经过点(2,6),且与直线 ![]() 相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com