练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD最小时，∠PCD=（　　）
    A、60°B、90°
    C、45°D、75°
    考点：轴对称-最短路线问题
    专题：
    分析：根据当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC即可得出∠PCD的度数．
    解答：解：∵当PC+PD最小时，作出D点关于MN的对称点，正好是A点，
    连接AC，AC为正方形对角线，根据正方形的性质得出∠PCD=45°，
    ∴∠PCD=45°．
    故选C．
    点评：此题主要考查了轴对称求最短路线问题，根据已知得出D点关于MN的对称点，正好是A点是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    根据下面的两种移动电话计费方式表，考虑下列问题
    方式一方式二
    月租费30元/月0
    本地通话费0.30元/分钟0.40元/分钟
    （1）一个月内在本地通话200分钟，按方式一需交费多少元？按方式二呢？
    （2）对于某个本地通话时间，会出现按两种计费方式收费一样多吗？
    （3）如果你的爸爸新买一部手机，你会怎样帮他选择哪种计费方式？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程：
    （1）x2+2x=2；  
    （2）（x+3）（x-1）=5； 
    （3）（y-1）2+2y（y-1）=0；     
    （4）（2x+3）2=x2-8x+16．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线AB、CD相交于点O．OE平分∠AOD，若∠BOC=70°，则∠AOE的度数是（　　）
    A、20°B、35°
    C、70°D、110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

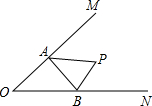    如图，已知∠MON=60°，P为∠MON内一点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数为（　　）度．
    A、40B、60
    C、100D、120

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，⊙O的直径CD垂直于弦AB，垂足为P，且AP=4cm，PD=2cm，则⊙O的半径为（　　）
    A、4cm
    B、5cm
    C、4
    		2
    cm
    D、2
    		3
    cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知∠α．
    （1）试画出∠α的一个余角（用∠1表示）和∠α的一个补角（用∠2表示）
    （2）若∠α=32°33′，则∠1=
     
    °；∠2=
     
    °．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

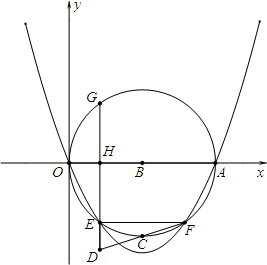    已知A是x轴正半轴上一个动点，以线段OA为直径作⊙B，圆心为点B，直径OA=m，线段EF是⊙B的一条弦，EF∥x轴，点C为劣弧EF的中点，过点E作DE垂直于EF，交抛物线C1：y=ax2+bx（a＞0）于点G，抛物线经过点O和点A．
    （1）求证：DG=m；
    （2）拖动点A，如果抛物线C1与⊙B除点O和点A外有且只有一个交点，求b的值；
    （3）拖动点A，抛物线C1交⊙B于点O、E、F、A，
    ①求证：DE=m-
    2
    a
    ；
    ②直接写出FC2的值（用a，m的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解方程组：
    （1）
    4x-3y=11
    2x+y=13
    ．          
    （2）
    2x-y=-4
    4x-5y=-23
    ．

    查看答案和解析>>

    同步练习册答案