
如图,已知抛物线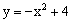 与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
问:△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理 由。
由。

解:∵抛物线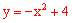 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,
 ∴A(2,0),B(0,4),即OA=2,OB=4。
∴A(2,0),B(0,4),即OA=2,OB=4。
∴tan∠OAB=2。
若△AON为等腰三角形,有三种情况:
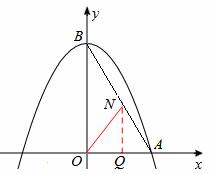
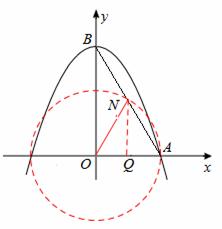
(I)若ON=AN ,如图1所示,
,如图1所示,
过点N作NQ⊥OA于点Q,
则Q为OA中点,OQ=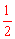 OA=1,
OA=1,
∴t=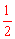 。
。

∴t=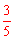 。
。
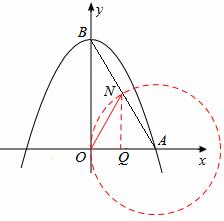
(III)若OA=AN,如图3所示,
过点N作NQ⊥OA于点Q,
设AQ=x,则AQ•tan∠O AB=2x,
AB=2x,
在Rt△AND中,由勾股定理得:NQ2+AQ2=AN2,
即 ,解得x1=
,解得x1=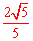 ,x2=
,x2= (舍去)
(舍去) 。
。
∴x=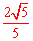 ,OD=2﹣x=2﹣
,OD=2﹣x=2﹣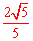 。
。
∴t=1﹣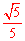 。
。
综上所述,当t为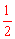 秒、
秒、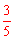 秒,1﹣
秒,1﹣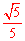 秒时,△AON为等腰三角形。
秒时,△AON为等腰三角形。
【考点】双动点问题,曲线上点的坐标与方程的关系,待定系数法,矩形的性质,等腰三角形的性质,勾股定理,解一元二次方程,分类思想的应用。



科目:初中数学 来源: 题型:
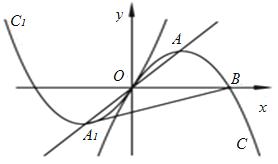
已知抛物线C: 过原点,与
过原点,与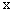 轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为
轴的另一个交点为B(4,0),A为抛物线C的顶点,直线OA的解析式为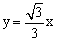 ,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。
,将抛物线C绕原点O旋转180°得到抛物线C1,求抛物线C、C1的解析式。
查看答案和解析>>
科目:初中数学 来源: 题型:
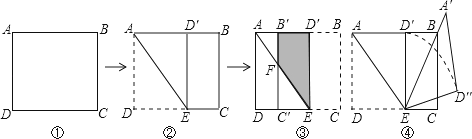
如图①,在矩形纸片ABCD中,AB=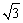
 +1,AD=
+1,AD=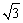
 .
.
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 ;
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四 边形B′C′ED′,B′C′交AE于点F
边形B′C′ED′,B′C′交AE于点F ,则四边形B′FED′的面积为 ;
,则四边形B′FED′的面积为 ;
(3)如图④ ,将图
,将图 ②中的△AE
②中的△AE D′绕点E顺时针旋转α角,得△A′ED″,使得EA′
D′绕点E顺时针旋转α角,得△A′ED″,使得EA′ 恰好经过顶点B,求弧D′D″的长.(结果保留π)
恰好经过顶点B,求弧D′D″的长.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP. 将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.
(1) 如图1,当0°<α<60°时,在α角变化过程中,△BEF与△AEP始终存在 关系(填“相似”或“全等”),并说明理由;
(2)如图2,设∠ABP=β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图3,当α=60°时,点E、F与点B重合. 已知AB=4,设DP=x,△A1BB1的面
积为S,求S关于x的函数关系式.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于 点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).
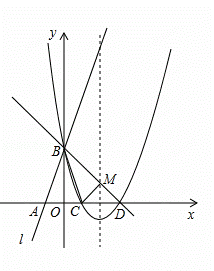

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以 点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,已知AB=AC=4,BC= ,且△ABC≌△DEF,将△DEF与△ABC重合在一起
,且△ABC≌△DEF,将△DEF与△ABC重合在一起 ,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
 腰三角形?若
腰三角形?若 能,求出
能,求出 △AEM的面积;若不能,请说明理由。
△AEM的面积;若不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
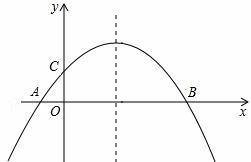
如图,抛物线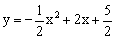 与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。
与x轴交于点A,B,与y轴交于点C。点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点 P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:
P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究: 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反 比例函数
比例函数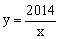 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式;
(3)若二次函数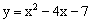 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com