
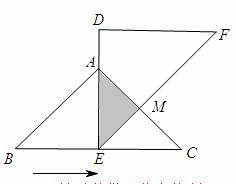
如图,在△ABC中,已知AB=AC=4,BC= ,且△ABC≌△DEF,将△DEF与△ABC重合在一起
,且△ABC≌△DEF,将△DEF与△ABC重合在一起 ,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
 腰三角形?若
腰三角形?若 能,求出
能,求出 △AEM的面积;若不能,请说明理由。
△AEM的面积;若不能,请说明理由。

解:能。
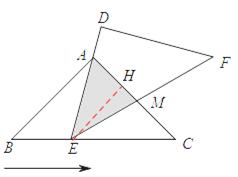
∵AB=AC=4,BC=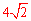 ,
,
∴AB2+AC2=BC2=32。
∴△ABC是等腰直角三角形。
∴∠C=450。
∵∠AEF=∠B=∠C,且∠AME>∠C,
∴∠AME>∠AEF。
∴AE≠AM。
当A E=EM时,如图1,则△A
E=EM时,如图1,则△A BE≌△ECM(SAS)。
BE≌△ECM(SAS)。
∴CE=AB=4。
∴CM=BE=BC﹣EC=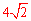 ﹣4。
﹣4。
∴ AM=6﹣
AM=6﹣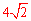 。
。
过点E作EH⊥AC于点H,则EH=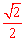 EC=
EC=
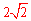 。
。
∴S△AEM=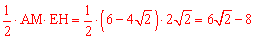 。
。

∴S△AEM=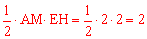 。
。
综上所述,当△AEM是等腰三角形时,△AEM的面积为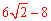 或2。
或2。
【考点】等腰直角三角形的判定和性质 ,勾股定理逆定理,全等、相
,勾股定理逆定理,全等、相 似三角形的判定和性质,三角形外角的性质,分类思想的应用。
似三角形的判定和性质,三角形外角的性质,分类思想的应用。



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
如图,在矩形ABCD中,AB=3,BC=4.动点P从点A出发沿AC向终点C运动,同时动点Q从点B出发沿BA向点A运动,到达A点后立刻以原来的速度沿AB返回.点P、Q运动速度均为每秒1个单位长度,当点P到达点C时停止运动,点Q也同时停止.连接PQ,设运动时间为t(t >0)秒.

(1)求线段AC的长度;
(2)当点Q从点B向点A运动时(未到达A点),求△APQ的面积S关于t的函数关系式,并写出t的取值范围;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线为l:
①当l经过点A时,射线QP交AD于点E,求AE的长;
②当l经过点B时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下列材料:
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值.

小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+P C值最小时PB的长.
C值最小时PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
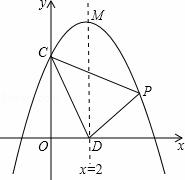
如图,在平面直角坐标系xOy中,抛物线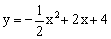 交y轴于点C
交y轴于点C ,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,
,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转, 与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知抛物线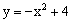 与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
与x轴交于点A,与y轴交于点B,动点Q从点O出发,以每秒2个单位长度的速度在线段OA上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒。
问:△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理 由。
由。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在平面直角坐标系中,四边形ABCO是梯形,且BC∥AO,其中A(6,0),B(3,
 ),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点
),∠AOC=60°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点 时,点Q也随之停止,设
时,点Q也随之停止,设 点P,Q运
点P,Q运 动的时间为t(秒).
动的时间为t(秒).
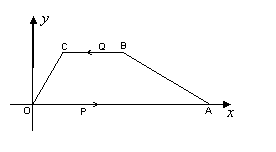

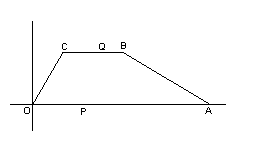

(1)求点C的坐标及梯形ABCO的面积;
 (2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(2)当点Q在CO边上运动时,求△OPQ的面积S与运动时间t的函数关系式,并写出自变量t的取值范围;
(3)以O,P,Q为顶点的三角形能构成直角三角形吗?若能,请求出t 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的 长;
长;
(2)设CP= x, △PDQ的面积为y,求y关于x的函数表达式, 并求自变量的取值范围;
x, △PDQ的面积为y,求y关于x的函数表达式, 并求自变量的取值范围;
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一根 木棒(AB)长为4,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,B端沿直线OM向右滑动到B′,与地面的倾斜角(∠A′
木棒(AB)长为4,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,B端沿直线OM向右滑动到B′,与地面的倾斜角(∠A′ B′O)为45°,则木棒中点从P随之运动到P′所经
B′O)为45°,则木棒中点从P随之运动到P′所经 过的路径长为 。
过的路径长为 。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com