
����Ŀ��Ϊ�˽���꼶Ů�����ʽ����仯���������������ʦ��ѧ�ڴӾ��꼶ȫ��240��Ů���������ȡ20��Ů���������ʲ��ԣ�����ȡ��20��Ů����ѧ�ڵ����ʲ��Գɼ����жԱȣ�����ʦ���������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
a. ���β��Գɼ����ٷ��ƣ���Ƶ���ֲ�ֱ��ͼ���£����ݷ��飺60��x��70��70��x��80��80��x��90��90��x��100����
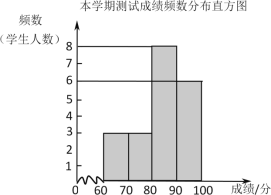
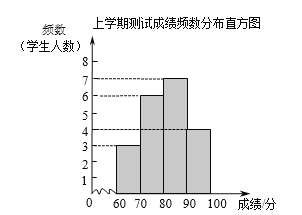
b.�ɼ���80��x��90���ǣ�
��ѧ�ڣ�80 81 85 85 85 86 88
��ѧ�ڣ�80 82 83 86 86 86 88 89
c. ����ѧ���������Գɼ���ƽ��������λ�����������£�
ѧ�� | ƽ���� | ��λ�� | ���� |
��ѧ�� | 84 | a | 85 |
��ѧ�� | b | c | d |
����������Ϣ���ش��������⣺
��1������a��ֵ�� ��
��2�����й��ڱ�ѧ���������Գɼ��Ľ��ۣ���c��86����d��86�����ɼ��ļ������Ϊ41����b�п��ܵ���80������������ȷ���۵������ ��
��3����������ͬ�Ƕȷ�����20��Ů������ѧ�ڵ���ѧ�����ʽ����仯�����
���𰸡���1��![]() ����2���٣���3������λ���Ͽ�������ѧ�ڵ�
����2���٣���3������λ���Ͽ�������ѧ�ڵ�![]() �ֵ���ѧ�ڵ�86�֣�����һ�����ϵ�Ů����������нϴ��������ӳɼ��ﵽ80�ֵ�Ů�����Ͽ�����ѧ�ڱ���ѧ������3�ˣ���90�����ϵĶ�2�ˣ���������ѵ����Ч�����𰸲�Ψһ����
�ֵ���ѧ�ڵ�86�֣�����һ�����ϵ�Ů����������нϴ��������ӳɼ��ﵽ80�ֵ�Ů�����Ͽ�����ѧ�ڱ���ѧ������3�ˣ���90�����ϵĶ�2�ˣ���������ѵ����Ч�����𰸲�Ψһ����
��������
��1�������������ݺ�ֱ��ͼ����λ���Ķ��弴�ɵã�
��2���ֱ����ƽ��������λ��������������Ķ�������жϼ��ɵã�
��3������λ����Ƶ���ֲ�ֱ��ͼ�ĽǶȷ������ɵã�
��1������λ���Ķ���ã���ѧ���������Գɼ�����С�����˳�������10�����͵�11������ƽ����Ϊ����λ��
��![]()
�ʴ�Ϊ��![]() ��
��
��2������λ���Ķ���ã���ѧ���������Գɼ�����С�����˳�������10�����͵�11������ƽ����Ϊ����λ��
��![]() �����ۢ���ȷ
�����ۢ���ȷ
�ɱ�ѧ�ڲ��Գɼ�Ƶ���ֲ�ֱ��ͼ��֪��![]() ������Ϊ3�ˣ�
������Ϊ3�ˣ�![]() ������Ϊ3�ˣ�
������Ϊ3�ˣ�![]() ������Ϊ8�ˣ�
������Ϊ8�ˣ�![]() ������Ϊ6��
������Ϊ6��
�ɼ���![]() ���ⲿ�������У�86���ֵĴ�����࣬Ϊ3�Σ�����
���ⲿ�������У�86���ֵĴ�����࣬Ϊ3�Σ�����![]() ����ijɼ����п���ij���ɼ��Ĵ�������3�Σ���
����ijɼ����п���ij���ɼ��Ĵ�������3�Σ���![]() ��һ������86�������ۢڴ���
��һ������86�������ۢڴ���
�ɼ���Ķ���ã���ѧ���������Գɼ��ļ�������ֵΪ![]()
����Գɼ��ļ������Ϊ41�������ۢ۴���
��![]() �ijɼ���Ϊ
�ijɼ���Ϊ![]() ��
��![]() �ijɼ���Ϊ
�ijɼ���Ϊ![]() ��
��![]() �ijɼ���Ϊ
�ijɼ���Ϊ![]() ��
��![]() �ijɼ���Ϊ
�ijɼ���Ϊ![]()
��![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]()
![]()
��![]()
��ƽ�����Ĺ�ʽ�ã�![]()
��![]()
��![]()
��ˣ�![]() û�п��ܵ���80�������ܴۢ���
û�п��ܵ���80�������ܴۢ���
���ϣ���ȷ���۵�����Ǣ�
�ʴ�Ϊ���٣�
��3������λ���Ͽ�������ѧ�ڵ�![]() �ֵ���ѧ�ڵ�86�֣�����һ�����ϵ�Ů����������нϴ�����
�ֵ���ѧ�ڵ�86�֣�����һ�����ϵ�Ů����������нϴ�����
�ӳɼ��ﵽ80�ֵ�Ů�����Ͽ�����ѧ�ڵ�����Ϊ![]() ����ѧ�ڵ�����Ϊ
����ѧ�ڵ�����Ϊ![]() ������ѧ�ڱ���ѧ������3�ˣ���90�����ϵĶ�2�ˣ���������ѵ����Ч����
������ѧ�ڱ���ѧ������3�ˣ���90�����ϵĶ�2�ˣ���������ѵ����Ч����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ն��衱�������������ز���ij����ר������ij��Ʒ�Ƶ��ն��裬�ɱ�Ϊ30Ԫ/�У�ÿ������![]() (��)�����۵���
(��)�����۵���![]() (Ԫ)֮�����һ�κ�����ϵ����ͼ��ʾ��
(Ԫ)֮�����һ�κ�����ϵ����ͼ��ʾ��
(1)��![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
(2)����涨ÿ������ն����������������240�У�������������Ĺ�����ҵ��������ÿ������������о��500Ԫ����ƶ����ᣬ�����۵���Ϊ����Ԫʱ��ÿ���ȡ�ľ����������������Ƕ��٣�(ע:������=������-���)
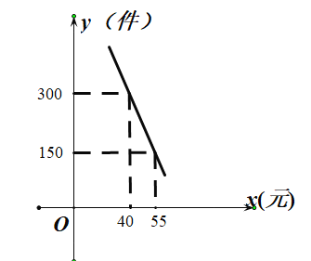
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ���е�
���е�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ����
�ֱ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ֱ��
��ֱ��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����������
����������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���õ�
���õ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �����Ϊ_______�����ú���������
�����Ϊ_______�����ú���������![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
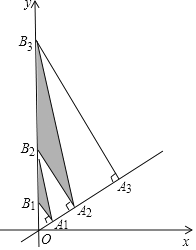
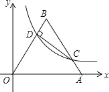
����Ŀ����ͼ�����߳�Ϊ10����������OAB������ƽ��ֱ������ϵxOy�У�C��AB���ϵĶ��㣨����˵�A��B�غϣ�����CD��OB�ڵ�D������C��D����˫����y��![]() �ϣ�k��0��x��0������k��ֵΪ��������
�ϣ�k��0��x��0������k��ֵΪ��������
A. 25![]() B. 18
B. 18![]() C. 9D. 9
C. 9D. 9![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
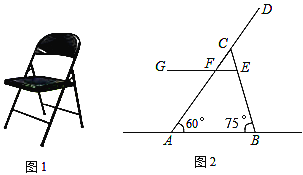
����Ŀ����ͼ1��һ���۵����ӣ�ͼ2��������ȫ��֧�Ⱥ�IJ���ʾ��ͼ��![]() ��ʾ�������ڵ�ֱ�ߣ�����
��ʾ�������ڵ�ֱ�ߣ�����![]() ��
��![]() ��ʾ�����ϴֵĸֹܣ�
��ʾ�����ϴֵĸֹܣ�![]() ��ʾ����ƽ�棬
��ʾ����ƽ�棬![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1��������![]() �ij���
�ij���
��2�����ʱ���ӵ����߶ȣ�����![]() ��ֱ��
��ֱ��![]() �ľ��룩��������������ţ�
�ľ��룩��������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
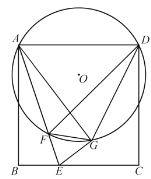
����Ŀ����������ABCD�У���E��BC����һ���㣬����AE����AE����ABE���۵á�AGE������DG������AGD����ӡ�O����O��AE�ڵ�F������FG��FD��
��1����֤��AGD����EFG��
��2����֤��ADF�ס�EGF��
��3����AB��3��BE��1�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬���P������Ϊ��x��y������x��0ʱ����P�ı任��P��������Ϊ����x��y������x��0ʱ����P�ı任��P��������Ϊ����y��x����
��1������A��2��1���ı任��A���ڷ���������y=![]() ��ͼ���ϣ���k=�� ����
��ͼ���ϣ���k=�� ����
��2������B��2��4�������ı任��B'��ֱ��y=ax+b�ϣ�������ֱ�߶�Ӧ�ĺ�����ϵʽΪ�� ������BOB���Ĵ�С���� ���ȣ�
��3����P��������y=x2��2x��3��ͼ���ϣ����߶�PP��Ϊ�Խ�����������PMP'N�����P�ĺ�����Ϊm����������PMP��N�ĶԽ��ߴ�ֱ��x��ʱ����m��ȡֵ��Χ��
��4��������y=��x��2��2+n��x�ύ�ڵ�C��D����C�ڵ�D����ࣩ������ΪE����P�ڸ��������ϣ�����P�ı任��P���������ߵĶԳ����ϣ����ı���ECP��D�����Σ���n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ����
����![]() ���㣬��
���㣬��![]() ���ڵ�
���ڵ�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �·���������һ���㣬����
�·���������һ���㣬����![]() ��
��
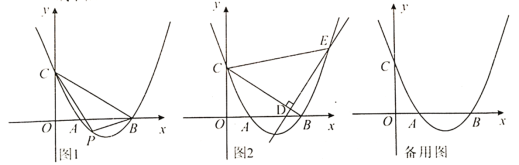
��1���������߽���ʽ��
��2���ڵ�![]() �ƶ������У�
�ƶ������У�![]() ������Ƿ�������ֵ�������ڣ��������������
������Ƿ�������ֵ�������ڣ��������������![]() �����꣬�������ڣ���˵�����ɣ�
�����꣬�������ڣ���˵�����ɣ�
��3�����![]() Ϊ
Ϊ![]() �ϲ���˵��غϵ�һ���㣬����
�ϲ���˵��غϵ�һ���㣬����![]() ���߶�
���߶�![]() �Ĵ��ߣ����������ڵ�
�Ĵ��ߣ����������ڵ�![]() ����
����![]() ��
��![]() ���ƣ���ֱ��д����
���ƣ���ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ���뷴��������y=![]() ��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��ͼ���ڵ�A����3��m+8����B��n����6�����㣮
��1����һ�κ����뷴���������Ľ���ʽ��
��2������AOB�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com