练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
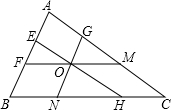
    已知O是△ABC内一点，且GN∥AB，FM∥BC，EH∥AC，求证：
    EH
    AC
    +
    FM
    BC
    +
    NG
    AB
    =2．
    考点：平行线分线段成比例
    专题：证明题
    分析：先证明△BEH∽△BAC得到
    EH
    AC
    =
    BH
    BC
    ，再证明△CGN∽△CAB得到
    NG
    AB
    =
    CN
    BC
    ，则
    EH
    AC
    +
    FM
    BC
    +
    NG
    AB
    =
    BH+CN+FM
    BC
    ，然后证明四边形BNOF和四边形CHOM都是平行四边形，可得FM=BN+CH，于是
    EH
    AC
    +
    FM
    BC
    +
    NG
    AB
    =
    BH+CN+BN+CH
    BC
    =2．
    解答：证明：∵EH∥AC，
    ∴△BEH∽△BAC，
    ∴
    EH
    AC
    =
    BH
    BC
    ，
    ∵GN∥AB，
    ∴△CGN∽△CAB，
    ∴
    NG
    AB
    =
    CN
    BC
    ，
    ∴
    EH
    AC
    +
    FM
    BC
    +
    NG
    AB
    =
    BH
    BC
    +
    FM
    BC
    +
    CN
    BC
    =
    BH+CN+FM
    BC
    ，
    ∵GN∥AB，FM∥BC，EH∥AC，
    ∴四边形BNOF和四边形CHOM都是平行四边形，
    ∴OF=BN，OM=CH，
    ∴FM=BN+CH，
    ∴
    EH
    AC
    +
    FM
    BC
    +
    NG
    AB
    =
    BH+CN+FM
    BC
    =
    BH+CN+BN+CH
    BC
    =
    2BC
    BC
    =2．
    点评：本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

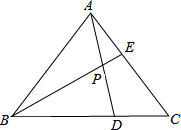    已知如图，在△ABC的边BC，AC上分别取点D、E，使BD=2CD，CE=2AE，AD与BE的交点为P，求证：S△EPA：S△APB：S△BPD：S△ABC=1：6：8：21．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

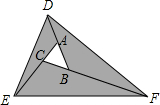    如图，已知△ABC，现将边BA延长至点D，使AD=AB，延长AC至点E，使CE=2AC．延长CB至点F，使BF=3BC，分别连结DE，DF，EF，得到△DEF，若△ABC的面积为1，则阴影部分的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

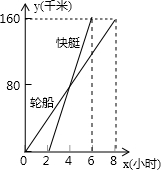    如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程随时间变化的图象．根据图象下列结论错误的是（　　）
    A、轮船的速度为20km/h
    B、快艇的速度为40km/h
    C、轮船比快艇先出发2h
    D、快艇不能赶上轮船

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把抛物线y=-x2+2x-1的图象向上平移m个单位，所得抛物线与x轴交点为A（x1，0），B（x2，0），且x1•x2=10．求平移后抛物线解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，DE∥FG∥BC，AD：DF：BF=1：2：3，BC=10cm．
    （1）求AE：EG：GC的值；
    （2）求DE与FH的比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小聪想利用树影测量树高，他在某时刻得小树的高为1.2m，树影的长为0.8m，但当他马上测得大树影时，因该大树在坡角为30°的斜坡附近，影子一部分落在水平地面上，一部分落在30度的斜坡上，他先测得水平地面上的影AB为3.4m，又测得斜坡上的影BC的长为2.8m，请你帮小聪测出树AD的高（精确到0.1m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    观察多项式mx+my+nx+ny，它的各项并没有公因式，也不能直接用公式法分解，那么通过观察发现，前两项有公因式m，后两项有公因式n，这样就把多项式分成两组，得到 m（x+y）+n（x+y），这样就会发现又有新的公因式（x+y），就可完成分解因式．分解的过程是：
    mx+my+nx+ny=（mx+my）+（nx+ny）=m（x+y）+n（x+y）=（m+n）（x+y）
    像这样把一个多项式进行分组来进行分解因式的方法叫做分组分解法，根据上面的例题来进行下列因式分解．
    （1）a2-b2-a-b；
    （2）4x2-4x-y2+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某商场销售一批衬衫，平均每天可售出20件，每件盈利20元，为了扩大销售量，增加盈利，尽快减少库存，商场决定采取适当的降价促销措施，经市场调查发现，如果每件衬衫降价1元，商场平均每天就可多售出2件，若商场平均每天要盈利432元，每件衬衫应降价多少元？

    查看答案和解析>>

    同步练习册答案