
【题目】如图,AB是⊙O的直径,点D是AB延长线上的一点,点C在⊙O上,且AC=CD,∠ACD=120°.
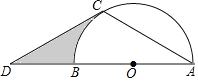
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,求图中阴影部分的面积.
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的AB边为圆O的弦,AC、BC分别交圆O于D、E,弧AD=弧BE,∠C=60°;

(1)求证:△ABC为等边三角形;
(2)如图2,F为弧AD上一点,连接FE并延长至G,连接BG,若∠AFB=∠G,求∠FBG的正弦值;
(3)如图3,在(2)的条件下,连接FC并延长交BG延长线于H,若CF=CH,AF=7,HG=12,求线段BF的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
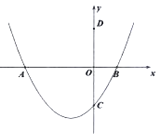
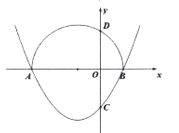
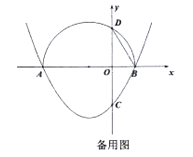
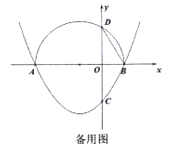
(1)直接写出抛物线的对称轴,及抛物线与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标;
的坐标;
(2)点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() ,当点
,当点![]() 在以
在以![]() 为直径的半圆上时,求抛物线的解析式;
为直径的半圆上时,求抛物线的解析式;
(3)在(2)的情况下,在抛物线上是否存在一点![]() ,使
,使![]() ,
,![]() ,
,![]() 三条之中,其中一条是另两条所夹角的角平分线?若存在,请求出点
三条之中,其中一条是另两条所夹角的角平分线?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8.则图中阴影部分的面积是( )
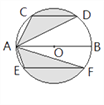
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆/小时)指单位时间内通过道路指定断面的车辆数;速度
(辆/小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米/小时)指通过道路指定断面的车辆速度,密度
(千米/小时)指通过道路指定断面的车辆速度,密度![]() (辆/千米)指通过道路指定断面单位长度内的车辆数.
(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度 | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
流量 | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确的是____.(只填上正确答案的序号)
关系最准确的是____.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() 满足
满足![]() .请结合(1)中选取的函数关系式继续解决下列问题.
.请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵;
在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离![]() (米)均相等,求流量
(米)均相等,求流量![]() 最大时
最大时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一圆弧形桥拱的圆心为![]() ,拱桥的水面跨度
,拱桥的水面跨度![]() 米,桥拱到水面的最大高度
米,桥拱到水面的最大高度![]() 为
为![]() 米.求:
米.求:

![]() 桥拱的半径;
桥拱的半径;
![]() 现水面上涨后水面跨度为
现水面上涨后水面跨度为![]() 米,求水面上涨的高度为________米.
米,求水面上涨的高度为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线的表达式为
中,抛物线的表达式为![]() ,线段AB的两个端点分别为A(1,2),B(3,2)
,线段AB的两个端点分别为A(1,2),B(3,2)
(1)若抛物线经过原点,求出![]() 的值;
的值;
(2)求抛物线顶点C的坐标(用含有m的代数式表示);
(3)若抛物线与线段AB恰有一个公共点,结合函数图象,求出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com