
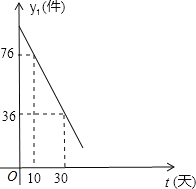
【题目】红星公司生产的某种时令商品每件成本为20元,经过市场调查发现,这种商品在未来40天内的日销售量y1(件)与时间t(天)的关系如图所示;未来40天内,每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=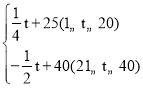 (t为整数);
(t为整数);
(1)求日销售量y1(件)与时间t(天)的函数关系式;
(2)请预测未来40天中哪一天的销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中该公司决定销售一件商品就捐赠a元(a为定值)利润给希望工程.公司通过销售记录发现,前20天中,第18天的时候,扣除捐赠后日销售利润为这20天中的最大值,求a的值.
【答案】(1)y=﹣2t+96;(2)第14天时,销售利润最大,为578元;(3)a=2.
【解析】
(1)从表格可看出每天比前一天少销售2件,所以判断为一次函数关系式;
(2)日利润=日销售量×每件利润,据此分别表示前20天和后20天的日利润,根据函数性质求最大值后比较得结论;
(3)列式表示前20天中每天扣除捐赠后的日销售利润,根据函数性质求a的取值.
解:(1)设一次函数为y=kt+b,
将(30,36)和(10,76)代入一次函数y=kt+b中,
有![]()
解得:.![]()
故所求函数解析式为y=﹣2t+96;
(2)设前20天日销售利润为W1元,后20天日销售利润为W2元.
由W1=(﹣2t+96)(![]() t+25﹣20)
t+25﹣20)
=(﹣2t+96)(![]() t+5)
t+5)
=﹣![]() t2+14t+480
t2+14t+480
=﹣![]() (t﹣14)2+578,
(t﹣14)2+578,
∵1≤t≤20,
∴当t=14时,W1有最大值578(元).
由W2=(﹣2t+96)(﹣![]() t+40﹣20)
t+40﹣20)
=(﹣2t+96)(﹣![]() t+20)
t+20)
=t2﹣88t+1920
=(t﹣44)2﹣16.
∵21≤t≤40,此函数对称轴是t=44,
∴函数W2在21≤t≤40上,在对称轴左侧,随t的增大而减小.
∴当t=21时,W2有最大值为(21﹣44)2﹣16=529﹣16=513(元).
∵578>513,故第14天时,销售利润最大,为578元;
(3)由题意得:W=(﹣2t+96)(![]() t+25﹣20﹣a)(1≤t≤20),配方得:
t+25﹣20﹣a)(1≤t≤20),配方得:
W=﹣![]() [t﹣2(a+7)]2+2(a﹣17)2(1≤t≤20)
[t﹣2(a+7)]2+2(a﹣17)2(1≤t≤20)
∵a为定值,而t=18时,W最大,
∴2(a+7)=18,解得:a=2


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
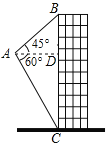
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为45°,测得底部C的角为60°,此时航拍无人机与该建筑物的水平距离AD为80m,那么该建筑物的高度BC为_____m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统文化与我们生活息息相关,中华传统文化包括古文古诗、词语、乐曲、赋、民族音乐、民族戏剧、曲艺、国画、书法、对联、灯谜、射覆、酒令、歇后语等.在中华优秀传统文化进校园活动中,某校为学生请“戏曲进校园”和民族音乐”做节目演出,其中一场“戏曲进校园”的价格比一场“民族音乐”节目演出的价格贵600元,用20000元购买“戏曲进校园”的场数是用8800元购买“民族音乐节目演出场数的2倍,求一场“民族音乐”节目演出的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
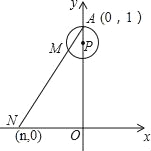
【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=![]() 时,n=_____;
时,n=_____;
(2)随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
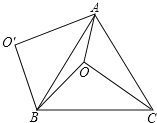
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O'的距离为8;③四边形AOBO'的面积为24+15![]() ; ④∠AOB=150°;⑤s△AOC+S△AOB=9
; ④∠AOB=150°;⑤s△AOC+S△AOB=9![]() +24,其中正确的结论是_____.
+24,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长张老师将901班和902班的成绩进行整理并绘制成如下的统计图:
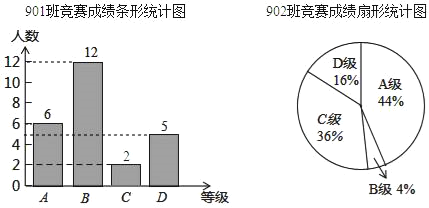
(1)在本次竞赛中,902班C级及以上的人数有多少?
(2)请你将下面的表格补充完整:
平均数(分) | 中位数(分) | 众数(分) | B级及以上人数 | |
901班 | 87.6 | 90 |
| 18 |
902班 | 87.6 |
| 100 |
|
(3)请你对901班和902班在本次竞赛中的成绩进行比较.
查看答案和解析>>
科目:初中数学 来源: 题型:
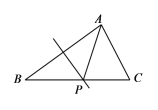
【题目】如图,在![]() 中,
中,![]() .
.
⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:![]() ;
;
⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com