
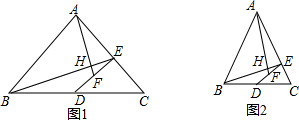
分析 连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=$\frac{1}{2}$∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得AD•CE=BD•DE.由此可得AD•CE=$\frac{1}{2}$BC•2DF=BC•DF,即$\frac{AD}{DF}=\frac{DE}{CE}$,由此可证到△AFD∽△BEC,则有$\frac{AF}{BE}=\frac{AD}{BC}$,在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-$\frac{1}{2}$∠BAC)=$\frac{AD}{BD}$=$\frac{2AD}{BC}$,从而可得$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的两个问题.
解答 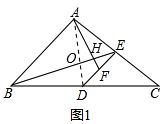 解:如图1,连接AD,
解:如图1,连接AD,
∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC=$\frac{1}{2}$∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴$\frac{AD}{BD}=\frac{DE}{CE}$,
即AD•CE=BD•DE.
∵点D是BC的中点,点F是DE的中点,
∴BD=$\frac{1}{2}$BC,DE=2DF,
∴AD•CE═$\frac{1}{2}$BC•2DF=BC•DF,
∴$\frac{AD}{DF}=\frac{DE}{CE}$,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴$\frac{AF}{BE}=\frac{AD}{BC}$,
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-$\frac{1}{2}$∠BAC,BD=$\frac{1}{2}$BC,
∴tan∠ABD=tan(90°-$\frac{1}{2}$∠BAC)=$\frac{AD}{BD}$=$\frac{2AD}{BC}$,
∴$\frac{AF}{BE}=\frac{AD}{BC}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$∠BAC).
∵△AFD∽△BEC,
∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°,
(1)如图1,
根据以上结论可得:
∠AHB=90°,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$×90°)=$\frac{1}{2}$;
∴AF⊥BE,$\frac{AF}{BE}$=$\frac{1}{2}$;
(2)如图2,
根据以上结论可得:∠AHB=90°,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$α);
∴AF⊥BE,$\frac{AF}{BE}$=$\frac{1}{2}$tan(90°-$\frac{1}{2}$α).
点评 本题主要考查的是相似三角形的判定与性质、三角函数的定义、等腰三角形的性质、同角的余角相等等知识,证到△AFD∽△BEC是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.
如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
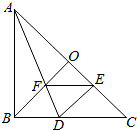 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
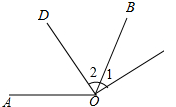 (1)已知一个角是它的余角的一半,求这个角的度数;
(1)已知一个角是它的余角的一半,求这个角的度数;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
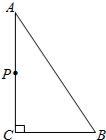 如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).
如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
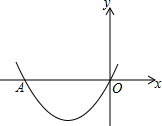 如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
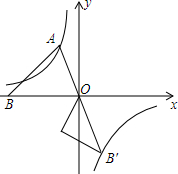 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com