
分析 (1)模仿例题利用完全平方公式即可解决.
(2)模仿例题利用完全平方公式以及立方和公式即可.
解答 解;(1)∵x2-4x+1=0,
∴x+$\frac{1}{x}$=4,
∴(x+$\frac{1}{x}$)2=16,
∴x2+2+$\frac{1}{{x}^{2}}$=16,
∴x2+$\frac{1}{{x}^{2}}$=14,
∴(x2+$\frac{1}{{x}^{2}}$)2=196,
∴x4+$\frac{1}{{x}^{4}}$+2=196,
∴x4+$\frac{1}{{x}^{4}}$=194.
故答案为4,14,194.
(2)∵2x2-7x+2=0,
∴x+$\frac{1}{x}$=$\frac{7}{2}$,x2+$\frac{1}{{x}^{2}}$=$\frac{41}{4}$,
∴${x^3}+\frac{1}{x^3}$=(x+$\frac{1}{x}$)(x2-1+$\frac{1}{{x}^{2}}$)=$\frac{7}{2}$×($\frac{41}{4}$-1)=$\frac{259}{8}$.
点评 本题考查一元一次方程的解、完全平方公式、立方和公式,解决问题的关键是灵活应用完全平方公式,记住两边平方不能漏项(利用完全平方公式整体平方),属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
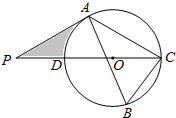 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
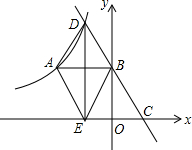 如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.
如图所示,在平面直角坐标系中,双曲线y=$\frac{k}{x}$(x<0)上有一点A(-2,2),AB⊥y轴于点B,点C是x轴正半轴上一动点,直线CB交双曲线于点D,DE⊥x轴于点E,连接AE,AD,BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
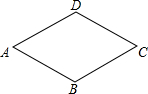 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 16$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com