
 如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°.
如图,两平面镜l,m的夹角为α,入射光线A0平行于m入射到l上,经过两次反射后射出的反射光线O′B与l平行,则∠α=60°. 分析 先根据平行线的性质与反射的性质得出△OO′C是等边三角形,由此可得出结论.
解答 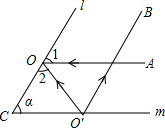 解:∵假设OA与l的锐角夹角是∠1,OO′与l的锐角夹角是∠2,根据平行线和反射的性质可知:∠1=∠2=∠α,
解:∵假设OA与l的锐角夹角是∠1,OO′与l的锐角夹角是∠2,根据平行线和反射的性质可知:∠1=∠2=∠α,
同理可知∠α=∠BO′m=∠OO′C.
∴△OO′C是等边三角形,
∴∠α的度数为60°.
故答案是:60°.
点评 本题考查的是平行线的性质定理1:两条平行线被第三条直线所截,同位角相等. 简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补..简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )
张萌取三个如图所示的面积为4cm2的钝角三角形按如图所示的方式相连接,拼成了一个正六边形,则拼成的正六边形的面积为( )| A. | 12cm2 | B. | 20cm2 | C. | 24cm2 | D. | 32cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
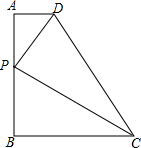 如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.
如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com