
分析 利用实数的运算法则和整式的运算法则即可求出答案.
解答 解:(1)原式=3.5-2.5-1.4-4.6=1-6=-5;
(2)原式=-4÷(-64)+0.2×$\frac{25}{4}$=$\frac{1}{16}$+$\frac{5}{4}$=$\frac{21}{16}$;
(3)原式=[$\frac{5}{2}$-(9+4-18)]÷5×(-1)=$\frac{15}{2}$÷5×(-1)=-$\frac{3}{2}$;
(4)原式=x-2x-2+3x=2x-2;
(5)原式=3x2+2xy-4y2-3xy+4y2-3x2=-xy;
(6)原式=4x2-20x-10x2-15x=-6x2-35x;
点评 本题考查运算能力,涉及实数运算,整式混合运算,考查学生的运算能力.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
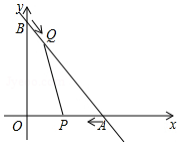 如图,直线y=-$\frac{4}{3}$x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
如图,直线y=-$\frac{4}{3}$x+8与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com