【题目】小敏家2017年和2018年的家庭支出如下：
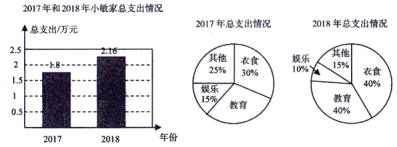
（1）2017年教育方面支出所占的百分比是多少？教育方面支出的金额是多少？
（2）2018年教育方面支出的金额是多少？教育方面支出对应的扇形圆心角度数是多少？
（3）2018年教育方面支出的金额比2017年增加了还是减少了？变化了多少？
【答案】（1）
，0.54万元；（2）0.864万元，
；（3）2018年教育方面支出的金额比2017年增加了
万元
【解析】
（1）根据扇形图即可得出2017年教育方面支出所占的百分比；再由条形图中总支出即可得出教育方面支出的金额；
（2）根据条形图中的总支出和扇形图中的2018年教育方面支出所占的百分比，即可得出其金额；由其所占百分比，即可得出其所对扇形圆心角；
（3）根据（1）（2）所得结论，进行比较计算即可.
（1）由图（2）可知
2017年教育方面支出所占的百分比是：
教育方面支出的金额是：1.8×30%=0.54万元
（2）2018年教育方面支出的金额是：
万元
教育方面支出对应的扇形圆心角度数是：
（3）2018年教育方面支出的金额比2017年增加了，
增加了：
万元
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
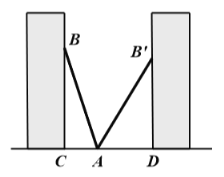
【题目】如图，小巷左右两侧是竖直的墙，一架梯子
斜靠在左墙时，梯子底端到左墙角的距离
为0.7米，顶端到地面距离
为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端到地面距离
为2米，求小巷的宽度
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于点E.
（1）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数.
（2）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（1）相同，求此时∠A1EC的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲，乙两人是某车间一个小组的同事，其中甲是老员工，每天可以制作零件160个．乙是新员工，每天可以制作零件80个．现有一个订单需要甲，乙合作制作2400个
零件．
（1）甲，乙合作多少天可以制作完这2400个零件；
（2）若开始制作时，甲临时有事需要请假2天，问制作这批订单的过程中，甲工作多少天时，制作的零件数恰好与乙制作的零件数相同．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
姓 名 | 1 | 2 | 3 | 4 | 5 |
小 王 | 60 | 75 | 100 | 90 | 75 |
小 李 | 70 | 90 | 80 | 80 | 80 |
根据上表解答下列问题：
(1)完成下表：
姓 名 | 平均成绩（分） | 中位数（分） | 众数（分） | 方差 |
小 王 | 75 | 190 | ||
小 李 | 80 | 80 |
(2)在这五次测试中，成绩比较稳定的同学是谁？若将80分以上(含80分)的成绩视为秀，则小王、小李在这五次测试中的优秀率各是多少？
(3)历届比赛表明，成绩达到80分以上(含80分)就很可能获奖，成绩达到90分以上(含90分)就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，分别得到点A，B的对应点C，D，连接AC，BD，CD．
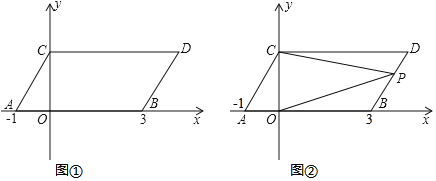
（1）求点C，D的坐标及S四边形ABDC；
（2）在y轴上是否存在一点Q，连接QA，QB，使S△QAB＝S四边形ABDC若存在这样一点，求出点Q的坐标；若不存在，试说明理由；
（3）如图②，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合），求证：∠DCP+∠BOP＝∠CPO．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
