
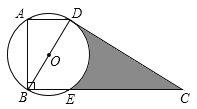
【题目】如图,在梯形ABCD中,![]() ,上底AD为
,上底AD为![]() ,以对角线BD为直径的
,以对角线BD为直径的![]() 与CD切于点D,与BC交于点E,且
与CD切于点D,与BC交于点E,且![]() 为
为![]() ,则图中阴影部分的面积为____.(结果保留根号)
,则图中阴影部分的面积为____.(结果保留根号)
科目:初中数学 来源: 题型:
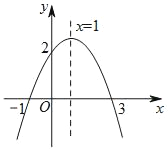
【题目】二次函数y=ax2+bx+c(a≠0,a,b,c为常数)图象如图所示,根据图象解答问题.
(1)写出过程ax2+bx+c=0的两个根.
(2)写出不等式ax2+bx+c>0的解集.
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇正在参加全国“数学竞赛”,只要他再答对最后两道单选题就能顺利过关,其中第一道题有3个选项,第二道题有4个选项,而这两道题嘉淇都不会,不过嘉淇还有一次“求助”没有使用(使用“求助”可让主持人去掉其中一题的一个错误选项).
(1)如果嘉淇第一题不使用“求助”,随机选择一个选项,那么嘉淇答对第一道题的概率是多少?
(2)若嘉淇将“求助”留在第二题使用,请用画树状图或列表法求嘉淇能顺利过关的概率;
(3)请你从概率的角度分析,建议嘉洪在第几题使用“求助”,才能使他过关的概率较大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于点E,O是AB上一点,经过A,E两点的⊙O交AB于点D,连接DE,作∠DEA的平分线EF交⊙O于点F,连接AF.
(1)求证:BC是⊙O的切线;
(2)若sin∠EFA=![]() ,AF=
,AF=![]() ,求线段AC的长.
,求线段AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是□ ABCD的对角线,延长BA至点E,使AE=AB,连接DE.
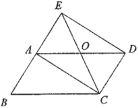
(1)求证:四边形ACDE是平行四边形;
(2)连接EC交AD于点O,若∠EOD=2∠B,求证:四边形ACDE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠C=90°,以 BC 为直径的⊙O 交 AB 于点 D,过点 D 作∠ADE=∠A,交 AC 于点 E.

(1)求证:DE 是⊙O 的切线;
(2)若![]() ,BC=15cm,求 DE 的长.
,BC=15cm,求 DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 分别在正方形
分别在正方形![]() 的边
的边![]() ,
,![]() 上,且
上,且![]() ,点
,点![]() 在射线
在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合).将线段
重合).将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
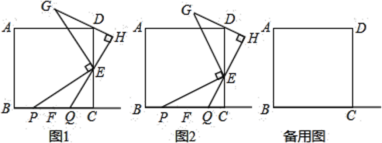
(1)如图1,若点![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,线段
上,线段![]() ,
,![]() ,
,![]() 的数量关系为 .
的数量关系为 .
(2)如图2,若点![]() 不是
不是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形![]() 的边长为6,
的边长为6,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
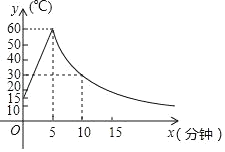
【题目】工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= ;
②下降阶段:当x>5时,y .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com