
ЁОЬтФПЁПAЁЂBСНЫљбЇаЃЕФбЇЩњЖМВЮМгСЫФГДЮЬхг§ВтЪдЃЌГЩМЈОљЮЊ7Љ10ЗжЃЌЧвЮЊећЪ§ЃЎССССЗжБ№ДгетСНЫљбЇаЃИїЫцЛњГщШЁвЛВПЗжбЇЩњЕФВтЪдГЩМЈЃЌЙВ200ЗнЃЌВЂЛцжЦСЫШчЯТЩаВЛЭъећЕФЭГМЦЭМЃЎ
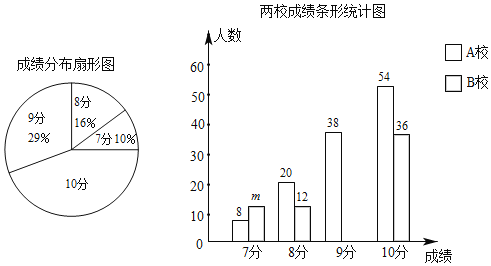
ЃЈ1ЃЉет200ЗнВтЪдГЩМЈЕФжаЮЛЪ§ЪЧЁЁ ЁЁЗжЃЌmЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛЩШаЮЭГМЦЭМжаЃЌЧѓГЩМЈЮЊ10ЗжЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЎ
ЃЈ3ЃЉССССЫуГіСЫЁА1УћAаЃбЇЩњЕФГЩМЈБЛГщЕНЁБЕФИХТЪЪЧ![]() ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ЃЌЧыФуЙРМЦAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМгаЖрЩйУћЃЎ
ЁОД№АИЁПЃЈ1ЃЉ9ЃЌ12ЃЛ,ЃЈ2ЃЉВЙЭММћНтЮіЃЌ162ЁуЃЛЃЈ3ЃЉ220ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжаЮЛЪ§ЕФЖЈвхМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉИљОнЩШаЮЭГМЦЭМжаЕФЪ§ОнВЙШЋЬѕаЮЭГМЦЭМЃЌНјЖјЕУЕНГЩМЈЮЊ10ЗжЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЌМДПЩЃЛ
ЃЈ3ЃЉЯШЫуГіAаЃзмШЫЪ§ЃЈ8+20+38+54ЃЉЁТ![]() ЃН1320ЃЈУћЃЉЃЌдйМЦЫуAаЃГЩМЈЮЊ8ЗжЕФбЇЩњЪ§,МДПЩЃЎ
ЃН1320ЃЈУћЃЉЃЌдйМЦЫуAаЃГЩМЈЮЊ8ЗжЕФбЇЩњЪ§,МДПЩЃЎ
ЃЈ1ЃЉгЩЬтвтЕУЃКАбетаЉГЩМЈАДДѓаЁХХСаКѓЃЌЕк100ЃЌ101 ЮЛЪ§ЖМЪЧ9ЗжЃЌЙЪжаЮЛЪ§ЪЧ9ЃЌ
mЃНЃЈ20+12ЃЉЁТ16%ЁС10%Љ8ЃН12ЃЈУћЃЉЃЛ
ЙЪД№АИЮЊЃК9ЃЌ12ЃЛ
ЃЈ2ЃЉBаЃГЩМЈЮЊ9ЗжЕФШЫЪ§ЮЊЃК200ЁС29%Љ38ЃН20ЃЈУћЃЉЃЌ
ВЙШЋЬѕаЮЭГМЦЭМШчЭМЫљЪОЃЛ
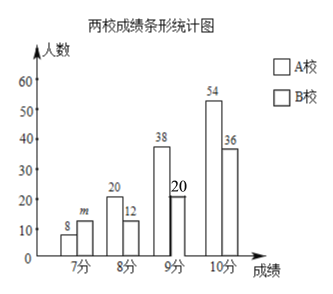
ГЩМЈЮЊ10ЗжЫљдкЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊ![]() ЁС360ЁуЃН162ЁуЃЛ
ЁС360ЁуЃН162ЁуЃЛ
ЃЈ3ЃЉгЩЬтвтПЩЕУЃКЃЈ8+20+38+54ЃЉЁТ![]() ЃН1320ЃЈУћЃЉЃЌ
ЃН1320ЃЈУћЃЉЃЌ
1320ЁС![]() ЃН220ЃЈУћЃЉЃЎ
ЃН220ЃЈУћЃЉЃЎ
Д№ЃКAаЃГЩМЈЮЊ8ЗжЕФбЇЩњДѓдМга220УћЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
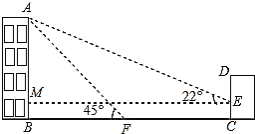
ЁОЬтФПЁПШчЭМЃЌФГАьЙЋТЅABЕФгвБпгавЛНЈжўЮяCDЃЌдкНЈЩшЮяCDРыЕиУц2УзИпЕФЕуEДІЙлВтАьЙЋТЅЖЅAЕуЃЌВтЕУЕФбіНЧ![]() =
=![]() ЃЌдкРыНЈЩшЮяCD 25УздЖЕФFЕуЙлВтАьЙЋТЅЖЅAЕуЃЌВтЕУЕФбіНЧ
ЃЌдкРыНЈЩшЮяCD 25УздЖЕФFЕуЙлВтАьЙЋТЅЖЅAЕуЃЌВтЕУЕФбіНЧ![]() =
=![]() ЃЈBЃЌFЃЌCдквЛЬѕжБЯпЩЯЃЉЃЎ
ЃЈBЃЌFЃЌCдквЛЬѕжБЯпЩЯЃЉЃЎ
ЃЈ1ЃЉЧѓАьЙЋТЅABЕФИпЖШЃЛ
ЃЈ2ЃЉШєвЊдкAЃЌEжЎМфЙввЛаЉВЪЦьЃЌЧыФуЧѓГіAЃЌEжЎМфЕФОрРыЃЎЃЈВЮПМЪ§ОнЃК![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНГЕЭЌЪБДг![]() ЕиГіЗЂЃЌбиЭЌвЛТЗЯпИїзддШЫйЯђ
ЕиГіЗЂЃЌбиЭЌвЛТЗЯпИїзддШЫйЯђ![]() ЕиааЪЛЃЌМзЕНДя
ЕиааЪЛЃЌМзЕНДя![]() ЕиЭЃСє1аЁЪБКѓАДдТЗвдСэвЛЫйЖШдШЫйЗЕЛиЃЌжБЕНгыввГЕЯргі.ввГЕЕФЫйЖШЮЊУПаЁЪБ60ЧЇУз.СНГЕжЎМфЕФОрРы
ЕиЭЃСє1аЁЪБКѓАДдТЗвдСэвЛЫйЖШдШЫйЗЕЛиЃЌжБЕНгыввГЕЯргі.ввГЕЕФЫйЖШЮЊУПаЁЪБ60ЧЇУз.СНГЕжЎМфЕФОрРы![]() ЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф
ЃЈЧЇУзЃЉгыввГЕааЪЛЪБМф![]() ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ
ЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈ ЃЉ
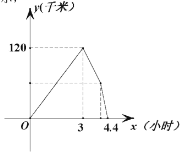
A.ааЪЛ3аЁЪБКѓЃЌСНГЕЯрОр120ЧЇУз
B.МзГЕДг![]() ЕН
ЕН![]() ЕФЫйЖШЮЊ100ЧЇУз/аЁЪБ
ЕФЫйЖШЮЊ100ЧЇУз/аЁЪБ
C.МзГЕЗЕЛиЪЧааЪЛЕФЫйЖШЮЊ95ЧЇУз/аЁЪБ
D.![]() ЁЂ
ЁЂ![]() СНЕижЎМфЕФОрРыЮЊ300ЧЇУз
СНЕижЎМфЕФОрРыЮЊ300ЧЇУз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гы
гы![]() жсЃЌ
жсЃЌ![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() СНЕуЃЌгыЗДБШР§КЏЪ§
СНЕуЃЌгыЗДБШР§КЏЪ§![]() НЛгкЕу
НЛгкЕу![]() Еу
Еу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЕу![]() ЕФзјБъЮЊ ЃЛ
ЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉШєЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЧѓЗДБШР§КЏЪ§
ЕФжаЕуЃЌЧѓЗДБШР§КЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЬѕМўЯТЃЌвд![]() ЮЊБпЯђгвзїе§ЗНаЮ
ЮЊБпЯђгвзїе§ЗНаЮ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() жБНгаДГі
жБНгаДГі![]() ЕФжмГЄгы
ЕФжмГЄгы![]() ЕФжмГЄЕФБШЃЎ
ЕФжмГЄЕФБШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§yЃН-x+1ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓгавЛИіНЛЕуЪЧA(-1ЃЌn)ЃЎ
ЕФЭМЯѓгавЛИіНЛЕуЪЧA(-1ЃЌn)ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉM(dЃЌ![]() )ЃЌN(dЃЌ
)ЃЌN(dЃЌ![]() )ЗжБ№ЪЧвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌШє
)ЗжБ№ЪЧвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌШє![]() ЃЌЧѓdЕФжЕЃЎ
ЃЌЧѓdЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
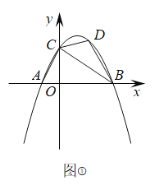
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() гыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
гыxжсНЛгкAЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
(1)ЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШчЭМЂйЃЌШєЕуDЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊmЃЈ0ЃМmЃМ3ЃЉЃЌСЌНгCDЃЌBDЃЌBCЃЌACЃЌЕБЁїBCDЕФУцЛ§ЕШгкЁїAOCУцЛ§ЕФ2БЖЪБЃЌЧѓmЕФжЕЃЛ
(3)ШєЕуNЮЊХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЧыдкЭМЂкжаЬНОПХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЪЙЕУвдBЃЌCЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
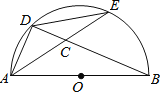
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌDЃЌEЪЧАыдВЩЯШЮвтСНЕуЃЌСЌНсADЃЌDEЃЌAEгыBDЯрНЛгкЕуCЃЌвЊЪЙЁїADCгыЁїABDЯрЫЦЃЌПЩвдЬэМгвЛИіЬѕМўЃЎЯТСаЬэМгЕФЬѕМўЦфжаДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛжБНЧзјБъЯЕжаЃЌКЏЪ§![]() КЭКЏЪ§
КЭКЏЪ§![]() (mЪЧГЃЪ§ЃЌЧв
(mЪЧГЃЪ§ЃЌЧв![]() )ЕФЭМЯѓПЩФмЪЧ( )
)ЕФЭМЯѓПЩФмЪЧ( )
A. 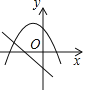 B.
B. 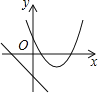
C.  D.
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуA(![]() ЃЌ4)ЃЌB(3ЃЌm)ЪЧжБЯпABгыЗДБШР§КЏЪ§
ЃЌ4)ЃЌB(3ЃЌm)ЪЧжБЯпABгыЗДБШР§КЏЪ§![]() ЃЈxЃО0ЃЉЭМЯѓЕФСНИіНЛЕуЃЎACЁЭxжсЃЌДЙзуЮЊЕуCЃЌвбжЊD(0ЃЌ1)ЃЌСЌНгADЃЌBDЃЌBCЃЎ
ЃЈxЃО0ЃЉЭМЯѓЕФСНИіНЛЕуЃЎACЁЭxжсЃЌДЙзуЮЊЕуCЃЌвбжЊD(0ЃЌ1)ЃЌСЌНгADЃЌBDЃЌBCЃЎ
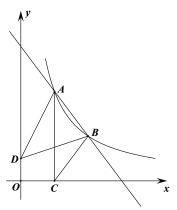
ЃЈ1ЃЉЧѓжБЯпABЕФБэДяЪНЃЛ
ЃЈ2ЃЉЁїABCКЭЁїABDЕФУцЛ§ЗжБ№ЮЊS1ЃЌS2ЃЌЧѓS2ЃS1ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com