

分析 (1)由直线解析式求出点E坐标,分点P在E点上方或下方两种情况讨论.三角形OPA面积等于$\frac{1}{2}$×OA×(±yp).
(2)将S=9代入(1)求得的一次函数解析式,即可求出点P的坐标.
(3)根据△COD≌△FOE,可知:OD=OE=8,OC=OF=6,因此求出C、D两点坐标,求出CD解析式,联立直线EF即可求出点P坐标.
解答 解:(1)令x=0,y=6,
∴F(0,6).
令y=0,x=-8,
∴E(-8,0).
当点P在x轴上方时,如下左图:此时,x>-6,
设P(x,$\frac{3}{4}$x+6),
则S=$\frac{1}{2}$×OA×yp,
=$\frac{1}{2}$×6×($\frac{3}{4}$x+6),
=$\frac{9}{4}$x+18.
当点P在x轴下方时,如下备用图,此时,x<-6,
设P(x,$\frac{3}{4}$x+6),
则S=$\frac{1}{2}$×OA×(-yp),
=$\frac{1}{2}$×6×(-$\frac{3}{4}$x-6),
=-$\frac{9}{4}$x-18.
综上所述:S=$\frac{9}{4}$x+18.(x>-6),S=-$\frac{9}{4}$x-18.(x<-6).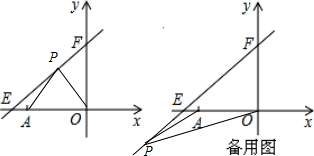
(2)令S=9代入S=$\frac{9}{4}$x+18得:x=-4,
将x=-4代入y=$\frac{3}{4}$x+6得y=3,
∴P(-4,3)
令S=9代入S=-$\frac{9}{4}$x-18得:x=-12,
将x=-12代入y=$\frac{3}{4}$x+6得y=-3,
∴P(-12,-3)
综上所述:P点坐标为(-4,3)或(-12,-3)
(3)存在
草图如下: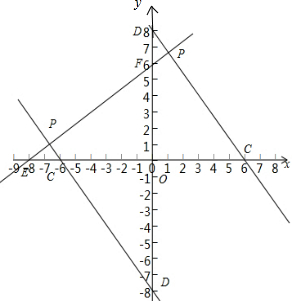
∵△COD≌△FOE,
∴OD=OE=8,OC=OF=6,
∴C(-6,0),D(0,-8),
或C(6,0),D(0,8),
当C(6,0),D(0,8),
设直线CD为y=kx+b,
带入C(6,0),D(0,8),
得:$\left\{\begin{array}{l}{6k+b=0}\\{b=8}\end{array}\right.$,
解得k=-$\frac{4}{3}$,b=8,
∴直线CD解析式:y=-$\frac{4}{3}$x+8.
同理当C(-6,0),D(0,-8)时,
直线CD解析式:y=-$\frac{4}{3}$x-8.
联立$\left\{\begin{array}{l}{y=\frac{3}{4}x+6}\\{y=-\frac{4}{3}x+8}\end{array}\right.$,
解得x=$\frac{24}{25}$,y=$\frac{168}{25}$.
∴P($\frac{24}{25}$,$\frac{168}{25}$).
同理求得另一点P(-$\frac{232}{25}$,-$\frac{24}{25}$).
∴存在这样的点P,使△COD≌△FOE,且P($\frac{24}{25}$,$\frac{168}{25}$)或(-$\frac{232}{25}$,-$\frac{24}{25}$).
点评 题目考查了一次函数综合应用、平面直角坐标系三角形面积求解、全等三角形等知识,题目整体较难,运算也相对复杂,对学生提出了很高的要求.同时在求解过程中,不要出现漏解现象.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
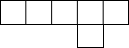 如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).
如图是由6个相同的正方形拼成的图形,请你将其中一个正方形移动到合适的位置,使它与另5个正方形能拼成一个正方体的表面展开图.(请在图中将要移动的那个正方形涂黑,并画出移动后的正方形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1和2 | B. | -1和-2 | C. | (-1,0)和(-2,0) | D. | (1,0)和(2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
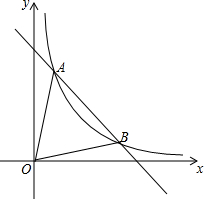 如图,一次函数y=-x+6的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+6的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com