
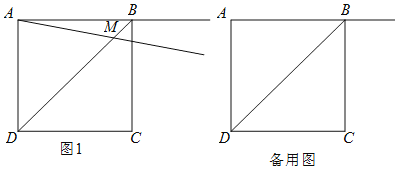
����Ŀ��������ABCD�ı߳�Ϊ2��������AB�Ƶ�A˳ʱ����ת���������������߶�BD���ڵ�M����CE��AM�ڵ�E����N���M����ֱ��CE�Գƣ�����CN��
��1����ͼ����0�㣼����45��ʱ��
�������ⲹȫͼ��
���õ�ʽ��ʾ��NCE���BAM֮���������ϵ��___________��
��2����45�㣼����90��ʱ��̽����NCE���BAM֮���������ϵ������֤����
��3����0�㣼����90��ʱ������AD���е�ΪF��ֱ��д���߶�EF�������ֵ��
���𰸡���1���ٲ�ͼ���������ڡ�NCE��2��BAM����2��![]() ��NCE+��BAM��90����֤������������3��1+
��NCE+��BAM��90����֤������������3��1+![]() ��
��
��������
��1����CE��AM�ڵ�E����N���M����ֱ��CE�Գ�������CN���ɡ�ABM�ա�CBM���ɵá�BAM����BCM���ɡ�ABC����CEA��90�㣬BC��AE����һ�����ɵá�BAM����BCE�����ɵõ���MCE��2��BAM���ɵ�N���M����ֱ��CE�Գ����ɵ�CN��CM�����ɵõ���NCE����MCE�������ó���NCE��2��BAM��
��2������CM���ж���ADM�ա�CDM�����ɵõ���DAM����DCM���ٸ��ݡ�DAQ����ECQ�����ɵõ���NCE����MCE��2��DAQ����![]() ���ٸ��ݡ�BAM����BCM����BCM+��DCM��90�㣬���ɵõ�
���ٸ��ݡ�BAM����BCM����BCM+��DCM��90�㣬���ɵõ�![]() ��
��
��3�����ݡ�CEA��90�㣬���ɵõ���E����ACΪֱ����Բ������EF����Բ��Oʱ�����ɵó��߶�EF�������ֵ��
��1������ȫ��ͼ����ͼ��ʾ��
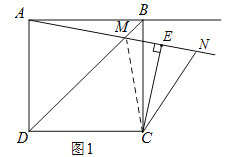
����NCE��2��BAM������������
��ͼ1������MC��
��ABCD������������AB=BC����ABM=��CBM��
��BM=BM�����ABM�ա�CBM�����BAM����BCM��
�ߡ�ABC����CEA��90�㣬BC��AE����һ�������BAM����BCE�����MCE��2��BAM��
����N���M����ֱ��CE�Գ�����CN��CM�����NCE����MCE�����NCE��2��BAM��
�ʴ�Ϊ����NCE��2��BAM��
��2��![]() ������������
������������
��ͼ������CM��
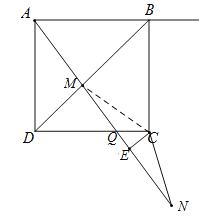
��AD��CD����ADM����CDM��DM��DM�����ADM�ա�CDM�����DAM����DCM��
�ߡ�ADQ����CEQ��90�㣬��AQD����CQE�����DAQ����ECQ�����NCE����MCE��2��DAQ����![]() ��
��
�ߡ�BAM����BCM����BCM+��DCM��90�㣬��![]() ��
��
��3����ͼ������CEA��90�㣬���E����ACΪֱ����Բ����OΪԲ��������ɵ���OF![]() CD��1��OE��OC
CD��1��OE��OC![]() AC
AC![]() ��
��
��OE+OF��EF���൱EF����Բ��Oʱ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����ƽ���ֳ�![]() �ȷݵ�ת�̣�ÿһ�������ж�������Ӧ�����֣��������˷ֱ�ת��ת�̣����ת��ת�̺�ָ����ָ�����ڵ�����Ϊ
�ȷݵ�ת�̣�ÿһ�������ж�������Ӧ�����֣��������˷ֱ�ת��ת�̣����ת��ת�̺�ָ����ָ�����ڵ�����Ϊ![]() ����ת��ת�̺�ָ����ָ�����ڵ�����Ϊ
����ת��ת�̺�ָ����ָ�����ڵ�����Ϊ![]() ����ָ���ڱ߽���ʱ����תһ�Σ�ֱ��ָ��һ������Ϊֹ����
����ָ���ڱ߽���ʱ����תһ�Σ�ֱ��ָ��һ������Ϊֹ����

![]() ֱ��д����ת��ת�̺���ָ�����ڵ�����Ϊ�����ĸ��ʣ�
ֱ��д����ת��ת�̺���ָ�����ڵ�����Ϊ�����ĸ��ʣ�
![]() ����״ͼ���б����������
����״ͼ���б����������![]() ���ڵڶ������ڵĸ��ʣ�
���ڵڶ������ڵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ƽ���ı��ν�Ƭ�ضԽ��������õ�ͼ���е����������ν�Ƭ![]() ��
��![]() ���������������ν�Ƭ�Ķ���B�붥��E�غϣ���
���������������ν�Ƭ�Ķ���B�붥��E�غϣ���![]() �Ƶ�B˳ʱ�뷽����ת����ʱAC��DF�ཻ�ڵ�O��
�Ƶ�B˳ʱ�뷽����ת����ʱAC��DF�ཻ�ڵ�O��
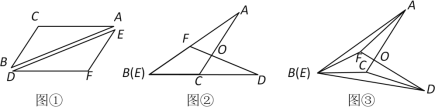
��1����![]() ��ת����ͼ��λ�ã���B��E����C,D��ͬһֱ����ʱ����AFD����DCA��������ϵ�� ��
��ת����ͼ��λ�ã���B��E����C,D��ͬһֱ����ʱ����AFD����DCA��������ϵ�� ��
��2����![]() ������ת����ͼ��λ��ʱ����1���еĽ��ۻ���������˵�����ɣ�
������ת����ͼ��λ��ʱ����1���еĽ��ۻ���������˵�����ɣ�
��3����ͼ���У�����BO,AD��̽��BO��AD֮����������λ�ù�ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���ͼ��Ķ��������ǣ�3��5�����������߾�����A��1��3����
��1����������ߵı���ʽ��
��2�������A���ڸ������߶Գ���ĶԳƵ���B�㣬����������y��Ľ�����C�㣬���ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
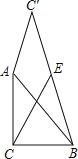
����Ŀ����ͼ����֪��ABC�У���ACB=90�㣬AC=BC=2����ֱ�DZ�AC��A����ʱ����ת��AC��������BC�䣬EΪBC�����е㣬����CE,��CE�����ֵΪ( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
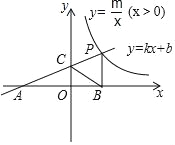
����Ŀ����ͼ��һ�κ���y��kx+b��ͼ���뷴��������y��![]() ��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC��BC��
��x��0����ͼ���ڵ�P��n��2������x�ύ�ڵ�A����4��0������y�ύ�ڵ�C��PB��x���ڵ�B����AC��BC��
��1����һ�κ����������������Ľ���ʽ��
��2������ͼ��ֱ��д��kx+b��![]() ��x��ȡֵ��Χ��
��x��ȡֵ��Χ��
��3������������ͼ�����Ƿ���ڵ�D��ʹ�ı���BCPDΪ���Σ�������ڣ������D�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
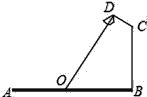
����Ŀ����ͼ��Ҫ�ڿ�ABΪ20��걺�������߰�װ·�ƣ�·�ƵĵƱ�CD�����BC��120���ǣ����ֵ�����DO��Ʊ�CD��ֱ�������ֵ�����DOͨ����··��������ߣ���OΪAB���е㣩ʱ����Ч����ѣ���CD=![]() �ף���·�Ƶĵ���BC�߶�Ӧ�����Ϊ____�ף��������������ţ���
�ף���·�Ƶĵ���BC�߶�Ӧ�����Ϊ____�ף��������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ����Ϊ����������·���г�����Ѳ��������ר�������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ���dz��˽��������Ƚ��˽������������˽���������̫�˽����ĸ��ȼ����ֱ����A��B��C��D�������ݵ��������Ƴ���ͼ��ʾ��������ͳ��ͼ������ͼ����Ϣ����������⣺
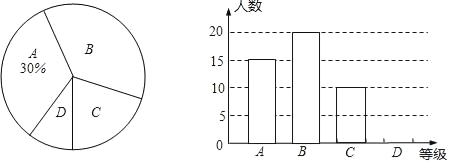
��1����������α������ѧ���������ˣ���������ͳ��ͼ����������
��2�����Ƹ�У1500��ѧ������C�ȼ�����ѧ���ж����ˣ�
��3������B�ȼ�����ѧ���У�����ѧ������4�ˣ�����1��3Ů������4�����У����ѡ��2�˽��вɷã�����ѡ��λͬѧ������ͬѧ�ĸ����Ƕ��٣������б�������״ͼ�ķ�����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��ͼ����������ABCD�У���E��F�ֱ���CD��BC�ϣ���BF=CE������BE��AF�ཻ�ڵ�G�������н��۲���ȷ���ǣ� ��

A��BE=AF B����DAF=��BEC C����AFB+��BEC=90�� D��AG��BE
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com