
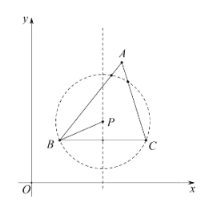
【题目】在平面直角坐标系xoy中,对于已知的△ABC,点P在边BC的垂直平分线上,若以P点为圆心,PB为半径的⊙P与△ABC三条边的公共点个数之和大于等于3,则称点P为△ABC关于边BC的“稳定点”.如图为△ABC关于边BC的一个“稳定点”P的示意图,已知A(m,0),B(0,n).
(1) 如图1,当![]() 时,在点
时,在点![]() 中,△AOB关于边OA的“稳定点”是________.
中,△AOB关于边OA的“稳定点”是________.
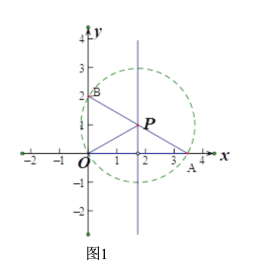
(2) 如图2,当n=4时,若直线y=6上存在△AOB关于边AB的“稳定点”,则m的取值范围是___________
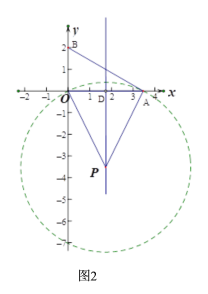
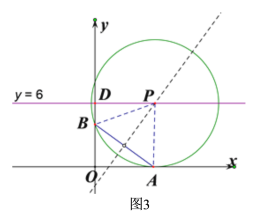
(3)如图3,当m=3,![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”,则k的取值范围是__________________.
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”,则k的取值范围是__________________.

【答案】(1)![]() ;(2)m>
;(2)m>![]() 或m<-
或m<-![]() ;(3)若1≤n<
;(3)若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.
【解析】
(1)分两种情况:①当⊙P过点B时,②当⊙P与直线AB相切时,分别求出点P的坐标,进而得到结论;
(2)分两种情况:①如图3,当点A在x轴的正半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,求出A的坐标,②如图4,当点A在x轴的负半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,求出A的坐标,进而即可得到结论;
(3)分6种情况:①如图5,若线段AB的中垂线过点M时,即![]() 时,②若1≤n<
时,②若1≤n<![]() 时,如图6,③若
时,如图6,③若![]() <n≤3时,④若3<n<
<n≤3时,④若3<n<![]() 时,⑤若n=
时,⑤若n=![]() 时,⑥若
时,⑥若![]() <n≤6时,分别求出k的求值范围,即可.
<n≤6时,分别求出k的求值范围,即可.
(1)①当⊙P过点B时,如图1,则OP=AP=BP,即:点P是AB的中点,此时,P(![]() ,1),
,1),
②当⊙P与直线AB相切时,如图2,切点为点A,则∠PAB=90°,
∵OA=![]() ,OB=2,∠AOB=90°,
,OB=2,∠AOB=90°,
∴∠BAO=30°,
∴∠OAP=60°,
∴DP=![]() AD=
AD=![]() ×
×![]() =3,
=3,
∴此时,P(![]() ,-3)
,-3)
综上所述,设点P的纵坐标为y,当-3<y≤1时,点P是△AOB关于边OA的“稳定点”,即:![]() 是△AOB关于边OA的“稳定点”.
是△AOB关于边OA的“稳定点”.
故答案是:![]() ;
;
(2)①如图3,当点A在x轴的正半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,
当n=4时,且⊙P与x轴相切,切点为点A,则∠PAO=90°,四边形PAOD是矩形,PA=OD=6,
∴PB=PA=6,BD=OD-OB=6-4=2,
∴PD=![]() =
=![]() ,
,
∴此时,A(![]() ,0),
,0),
∴当m>![]() 时,直线y=6上存在△AOB关于边AB的“稳定点”;
时,直线y=6上存在△AOB关于边AB的“稳定点”;
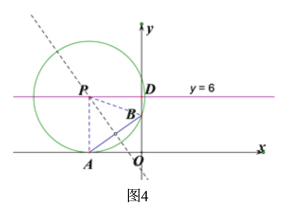
②如图4,当点A在x轴的负半轴时,以线段AB的中垂线与直线y=6的交点P为圆心,以PB的长为半径作⊙P,此时,A(-![]() ,0),
,0),
∴当m<-![]() 时,直线y=6上存在△AOB关于边AB的“稳定点”,
时,直线y=6上存在△AOB关于边AB的“稳定点”,
综上所述,m的取值范围是:m>![]() 或m<-
或m<-![]() .
.
故答案是:m>![]() 或m<-
或m<-![]() ;
;
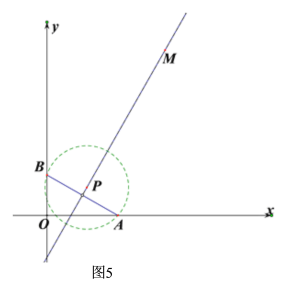
(3)①如图5,若线段AB的中垂线过点M时,即过点M(5,7)的直线y=kx+b与线段AB的中垂线重合,此时,符合条件.
把M(5,7)和AB的中点坐标(![]() ,
,![]() )代入y=kx+b,得
)代入y=kx+b,得 ,解得:
,解得: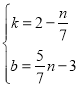 ,
,
设直线AB的解析式为:y=ax+c,则![]() ,解得:
,解得: ,
,
∴(![]() )(
)(![]() )=-1,解得:
)=-1,解得: ![]() ,
,![]() (舍去),
(舍去),
∴![]() ;
;
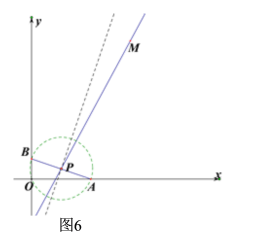
②若1≤n<![]() 时,如图6,当⊙P过点O时,P(
时,如图6,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
如图7,当⊙P与x轴相切,切点为点A,设OD=x,则AD=BD=3-x,
由勾股定理得:![]() ,解得:
,解得:![]() ,
,
∴AD=3-x=3-![]() =
=![]() ,
,
∵∠APD+∠ADP=∠ADP+∠BAO=90°,
∴∠APD=∠BAO,
∴tan∠APD=tan∠BAO,
∴![]() ,解得:AP=
,解得:AP=![]() ,
,
∴P(3,![]() ),
),
∴k=![]() ,
,
∴![]() <k≤
<k≤![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
③若![]() <n≤3时,当⊙P过点O时,P(
<n≤3时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与x轴相切,切点为点A,此时P(3,![]() ),k=
),k=![]() ,
,
∴![]() ≤k<
≤k<![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
④若3<n<![]() 时,当⊙P过点O时,P(
时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与y轴相切,切点为点B,此时⊙P的半径=![]() ,P(
,P(![]() ,n),k=
,n),k=![]() ,
,
∴![]() ≤k<
≤k<![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
⑤若n=![]() 时,则
时,则![]() ≤k时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
≤k时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
⑥若![]() <n≤6时,当⊙P过点O时,P(
<n≤6时,当⊙P过点O时,P(![]() ,
,![]() ),此时,
),此时,![]() ,
,
当⊙P与y轴相切,切点为点B,此时⊙P的半径=![]() ,P(
,P(![]() ,n),k=
,n),k=![]() ,
,
∴k<![]() 或k≥
或k≥![]() 时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
时,过点M(5,7)的直线y=kx+b上存在△AOB关于边AB的“稳定点”;
综上所述:若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.
故答案是:若1≤n<![]() 时,
时,![]() <k≤
<k≤![]() ;若
;若![]() 时,
时,![]() ;若
;若![]() <n≤3时,
<n≤3时,![]() ≤k<
≤k<![]() 时,若3<n<
时,若3<n<![]() 时,
时,![]() ≤k<
≤k<![]() ;若n=
;若n=![]() 时,
时,![]() ≤k;若
≤k;若![]() <n≤6时,k<
<n≤6时,k<![]() 或k≥
或k≥![]() .
.


科目:初中数学 来源: 题型:
【题目】由边长相等的小正方形组成的网格,以下各图中点A、B、C、D都在格点上.
(1)在图1中,PC:PB= ;
(2)利用网格和无刻度的直尺作图,保留痕迹,不写作法.
①如图2,在AB上找点P,使得AP:PB=1:3;
②如图3,在BC上找点P,使得△APB∽△DPC;
③如图4,在△ABC中内找一点P,连接PA、PB、PC,将△ABC分成面积相等的三部分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )
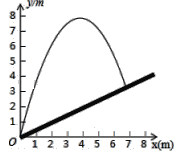
A.斜坡的坡度为1: 2
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.当小球抛出高度达到7.5m时,小球距O点水平距离为3m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全国人民每天都很关心新型冠状病毒感染肺炎的全国疫情和湖北疫情,下面是2020年2月7日小明在网上看到的2020年2月6日有关全国和武汉的疫情统计图表:
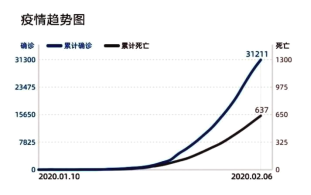
图1全国疫情趋势图
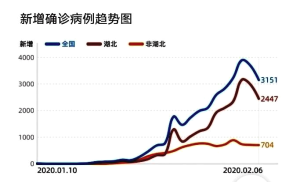
图2新增确诊病例趋势图
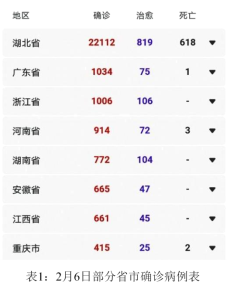
根据统计图表提供的信息,下列推断不合理的是( )
A.从图1可得出在2月6日的全国确诊病例达到3万多,是“非典”确诊病例(共5327例)的若干倍,说明新型冠状病毒比“非典”病毒传染性强.
B.从图2可得出在2月6日新增病例出现下降,说明此时全国的累计确诊病例开始下降,肺炎疫情得到控制,政府和人民的防疫工作有了显著成效
C.从图2在2月6日新增病例出现下降,可以估计2月6日后全国新型冠状病毒肺炎累计确诊病例的单日增长率会低于10%.
D.从表1可看出确诊病例较多的省市大部分都是在湖北周围,很大原因是由于携带病毒的流动人口造成的,所以控制疫情的有效手段是在家隔离,同时也可以推断在新疆和甘肃等西北地区疫情相对缓和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() (x>0)的图象与直线l1:
(x>0)的图象与直线l1:![]() 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.

(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数![]() (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() (x>0)的图象与直线l1:
(x>0)的图象与直线l1:![]() 交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.
交于点A,与直线l2:x=k交于点B.直线l1与l2交于点C.

(1) 当点A的横坐标为1时,则此时k的值为 _______;
(2) 横、纵坐标都是整数的点叫做整点. 记函数![]() (x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
(x>0) 的图像在点A、B之间的部分与线段AC,BC围成的区域(不含边界)为W.
①当k=3时,结合函数图像,则区域W内的整点个数是_________;
②若区域W内恰有1个整点,结合函数图象,直接写出k的取值范围:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(a﹣1)x2+3ax+1图象上的四个点的坐标为(x1,m),(x2,m),(x3,n),(x4,n),其中m<n.下列结论可能正确的是( )
A.若a>![]() ,则 x1<x2<x3<x4
,则 x1<x2<x3<x4
B.若a>![]() ,则 x4<x1<x2<x3
,则 x4<x1<x2<x3
C.若a<﹣![]() ,则 x1<x3<x2<x4
,则 x1<x3<x2<x4
D.若a<﹣![]() ,则 x3<x2<x1<x4
,则 x3<x2<x1<x4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国诗词大会》以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱.某学校为了提高学生的诗词水平,倡导全校3000名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的条形和扇形统计图如图所示.
(整理、描述数据):

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”:
一周诗词背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 16 | 24 | 32 | 78 |
| 35 |
(分析数据):
平均数 | 中位数 | 众数 | |
大赛之前 | 5 |
|
|
大赛之后 | 6 | 6 | 6 |
请根据调查的信息
(1)补全条形统计图;
(2)计算![]() 首,
首,![]() 首,
首,![]() 首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
首,并估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)根据调査的相关数据,选择适当的统计量评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并按要求完成相应的任务.

任务:
(1)如图2,是5×5的正方形网格,且小正方形的边长为1,利用“皮克定理”可以求出图中格点多边形的面积是 ;
(2)已知:一个格点多边形的面积S为15,且边界上的点数b是内部点数a的2倍,则a+b= ;
(3)请你在图3中设计一个格点多边形(要求:①格点多边形的面积为8;②格点多边形是一个轴对称图形但不是中心对称图形)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com