
分析 (1)根据销售利润y=(每千克销售价-每千克成本价)×销售量w,即可列出y与x之间的函数关系式;
(2)先利用配方法将(1)的函数关系式变形,再利用二次函数的性质即可求解;
解答 解:(1)y=w(x-6)
=(x-6)(-3x+60)
=-3x2+78x-360,
则y=-3x2+78x-360.
由题意,有$\left\{\begin{array}{l}{x≥6}\\{-3x+60≥0}\end{array}\right.$,
解得6≤x≤20.
故y与x的函数关系式为:y=-3x2+78x-360,自变量x的取值范围是6≤x≤20;
(2)∵y=-3x2+78x-360=-3(x-13)2+147,
∵a=-3<0,
∴当x<13时,y随x的增大而增大,
∵销售价格不得高于12元/个.
∴当x=12时,y有最大值144元.
故当销售价定为12元/千克时,每天可获最大销售利润144元.
点评 本题考查了二次函数的应用,难度适中.得到每天的销售利润的关系式是解决本题的关键,利用配方法或公式法求解二次函数的最值问题是常用的解题方法.


科目:初中数学 来源: 题型:解答题
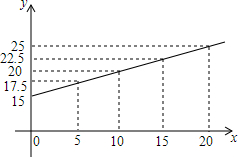 如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
如图是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
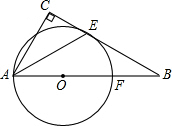 如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是30°.
如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是30°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,所有正方形的中心均在坐标原点O,且各边均与x轴成y轴平行,从内到外,它们的边长依次是2,4,6,8,…,每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8;…,则顶点A10的坐标为(-3,3).
如图,所有正方形的中心均在坐标原点O,且各边均与x轴成y轴平行,从内到外,它们的边长依次是2,4,6,8,…,每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4,A5,A6,A7,A8;…,则顶点A10的坐标为(-3,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
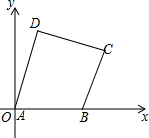 如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)
如图,在平面直角坐标系中,四边形各顶点的坐标分别为:A(0,0),B(7,0),C(9,5),D(2,7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com