
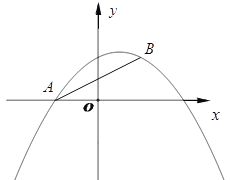
【题目】如图,已知抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
(1)求抛物线的解析式;
(2)阅读理解:在同一平面直角坐标系中,直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),直线
),直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),若
),若![]() ,则
,则![]() .
.
解决问题:①若直线![]() 与直线
与直线![]() 互相垂直,求
互相垂直,求![]() 的值;
的值;
②在抛物线上是否存在点![]() ,使得△PAB是以
,使得△PAB是以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是抛物线上一动点,且在直线
是抛物线上一动点,且在直线![]() 的上方(不与
的上方(不与![]() 、
、![]() 重合),求点
重合),求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
【答案】(1) y=-![]() x2+
x2+![]() x+1;(2)① -
x+1;(2)① -![]() ;②存在,点P的坐标(6,-14)或(4,-5);(3)
;②存在,点P的坐标(6,-14)或(4,-5);(3)![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)①利用垂线间的关系![]() ,即可求出m的值;
,即可求出m的值;
②分两种情况:当PA⊥AB时;当PB⊥AB时。根据垂线间的关系,可得PA,PB的解析式,根据解方程组,可得P点坐标;
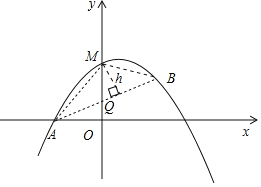
(3)作MQ⊥x轴交AB于Q。设M的横坐标为t,根据垂直于x轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,用t表示出MQ,于是可表示出三角形ABM的面积,是一个二次函数,根据二次函数的性质,可得面积的最大值,根据三角形的底一定时面积与高成正比,可得三角形高的最大值.
解:(1)将A,B点坐标代入,得
![]() ,
,
解得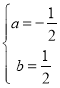 ,
,
所以抛物线的解析式为![]() ;
;
(2)①由直线y=2x-1与直线y=mx+2互相垂直,得
2m=-1,
即![]() ;
;
故答案为:![]() ;
;
②AB的解析式为![]() ,
,
当PA⊥AB时,PA的解析式为y=-2x-2,
联立PA与抛物线,得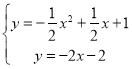 ,
,
解得![]() (舍),
(舍),![]() ,
,
即P(6,-14);
当PB⊥AB时,PB的解析式为y=-2x+3,
联立PB与抛物线,得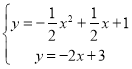 ,
,
解得![]() (舍去),
(舍去),![]() ,
,
即P(4,-5),
综上所述:△PAB是以AB为直角边的直角三角形,点P的坐标为(6,-14)(4,-5);
(3)如图:作MQ⊥x轴交AB于Q。
 ,
,
![]() ,
,
![]()
S△MAB=![]() MQ|xB-xA|
MQ|xB-xA|
![]()
=![]() ,
,
![]() 当t=0时,S取最大值
当t=0时,S取最大值![]() ,即M(0,1).
,即M(0,1).
由勾股定理,得
![]() ,
,
设M到AB的距离为h,由三角形的面积,得
![]()
点M到直线AB的距离的最大值是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC与BD相交于点O,AB=4,BD=4![]() ,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )
,E为AB的中点,点P为线段AC上的动点,则EP+BP的最小值为( )

A. 4B. 2![]() C. 2
C. 2![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
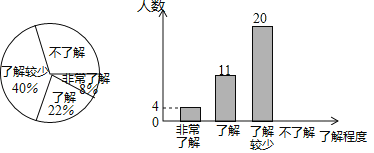
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是一个地球仪及它的平面图,在平面图中,点A、B分别为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所夹的角度约为67°,半径OC所在的直线与放置它的平面垂直,垂足为点E,DE=15cm,AD=14cm.

(1)求半径OA的长(结果精确到0.1cm,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
(2)求扇形BOC的面积(π取3.14,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
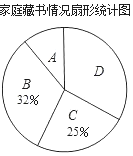
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
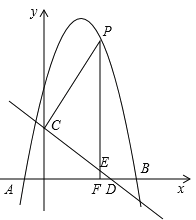
【题目】如图,抛物线![]() 与
与![]() 轴交于A (-1,0),B (5,0)两点,直线
轴交于A (-1,0),B (5,0)两点,直线![]() 与y轴交于点
与y轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是x轴上方的抛物线上一动点,过点
是x轴上方的抛物线上一动点,过点![]() 作
作![]() ⊥
⊥![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
(1)求抛物线的解析式;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,是否存在点
的对称点,是否存在点![]() ,使点
,使点![]() 落在
落在![]() 轴上?若存在,请直接写出相应的点
轴上?若存在,请直接写出相应的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com