

���� ��1������A��3��0����B��4��1���������ô���ϵ��������κ�������ʽ�������ó���C�����ꣻ
��2�����ݵ�A��B��C��������������BAC=90�㣬�Ӷ��õ���ABC����ֱ�������Σ����Ե�C��Ϊ�����һ����P�ģ��ٸ���ƽ��ֱ�ߵĽ���ʽ��kֵ����������B��ֱ��PB����������������⼴�ɵõ���һ����P��
��3�����ݵ�A��B��C������ɵá�OAE=��OAF=45�㣬�ٸ�����ͬԲ���Բ�У�ͬ�����Ե�Բ�ܽ���ȿɵá�OEF=��OFE=45�㣬��EOF=90��Ȼ����ݵȽǶԵȱ߿ɵ�OE=OF��Ȼ������ֱ��AC�Ľ���ʽ�����E�����꣬�����ù��ɶ�����ʾ��OE��ƽ����Ȼ�����������ε������ʽ��ʽ�������ɵõ�����ı���ʽ�������ö��κ�������ֵ�����ɣ�
��� �⣺��1������������y=ax2+bx+3��a��0������A��3��0����B��4��1�����㣬
��$\left\{\begin{array}{l}{9a+3b+3=0}\\{16a+4b+3=1}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{5}{2}}\end{array}\right.$��
�������߽���ʽΪ��y=$\frac{1}{2}$x2-$\frac{5}{2}$x+3��
��x=0����y=3��
���ԣ���C������Ϊ��0��3����
��2��������ڣ��������������ͼ1���ٹ���B��BH��x���ڵ�H��
��A��3��0����C��0��3����B��4��1����
���OCA=45�㣬��BAH=45�㣬
���BAC=180��-45��-45��=90�㣬
���ABC��ֱ�������Σ�
��C��0��3������������
���ԣ�P1��0��3����
�ڵ���ABP=90��ʱ������B��BP��AC���������ڵ�P��
��A��3��0����C��0��3����
��ֱ��AC�Ľ���ʽΪy=-x+3��
��ֱ��BP�Ľ���ʽΪy=-x+b��
��-4+b=1��
���b=5��
��ֱ��BP��y=-x+5��
����$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{1}{2}{x}^{2}-\frac{5}{2}x+3}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=6}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=1}\end{array}\right.$��
�֡ߵ�B��4��1����
���P��������-1��6����
�������������ڵ�P1��0��3����P2��-1��6����
��3����ͼ2����A��3��0����C��0��3����B��4��1����
���OAE=45�㣬��OAF=��BAH=45�㣬
�֡ߡ�OFE=��OAE����OEF=��OAF��
���OEF=��OFE=45�㣬
��OE=OF����EOF=180��-45���2=90�㣬����OEF��ֱ�������Σ�
�ߵ�E��ֱ��AC�ϣ�y=-x+3��
�����E��x��-x+3����
���ݹ��ɶ�����OE2=x2+��-x+3��2��
=2x2-6x+9��
���ԣ�S��OEF=$\frac{1}{2}$OE•OF=$\frac{1}{2}$OE2=x2-3x+$\frac{9}{2}$=��x-$\frac{3}{2}$��2+$\frac{9}{4}$��
���ԣ���x=$\frac{3}{2}$ʱ��S��OEFȡ��Сֵ$\frac{9}{4}$��
��ʱ-x+3=-$\frac{3}{2}$+3=$\frac{3}{2}$��
���ԣ���E�����꣨$\frac{3}{2}$��$\frac{3}{2}$����
���� ������Ҫ�����˶��κ������ۺϣ���Ҫ��������������x��Ľ����ľ���ı�ʾ���������ϵ������������ֱ�������ε��ж�����ͬԲ���Բ�У�ͬ�����Ե�Բ�ܽ���ȵ����ʣ���3���⣬���ݵ�A��B��C���������45��ǣ��Ӷ��õ�ֱ�ǻ���ȵĽ��ǽ���Ĺؼ�����Ŀ��˼������������


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x��x+3��2 | B�� | 2x��x-3��2 | C�� | 2x��x2-9�� | D�� | 2x��x+3����x-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
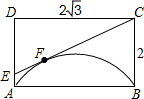 ��ͼ������ABCD�У�AB=2$\sqrt{3}$��AD=2����ABΪ���ھ����ڲ���һ��120��Ļ�������C��ֱ��CE����$\widehat{AB}$���ڵ�F����AD�߽��ڵ�E����ôDE�ij���-18+8$\sqrt{6}$��
��ͼ������ABCD�У�AB=2$\sqrt{3}$��AD=2����ABΪ���ھ����ڲ���һ��120��Ļ�������C��ֱ��CE����$\widehat{AB}$���ڵ�F����AD�߽��ڵ�E����ôDE�ij���-18+8$\sqrt{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com