
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为 ![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
【答案】
(1)解:设袋中黄球的个数为x个,
根据题意得 ![]() =
= ![]() ,
,
解得x=1,
所以袋中黄球的个数为1个;
(2)解:画树状图为:

共有12种等可能的结果数,其中两次摸出的都是红球的结果数为2,
所以两次摸出的都是红球的概率= ![]() =
= ![]()
【解析】(1)袋中黄球的个数为x个,根据概率公式得到 ![]() =
= ![]() ,然后利用比例性质求出x即可;(2)先画树状图展示所有12种等可能的结果数,再找出两次摸出的都是红球的结果数,然后根据概率公式计算即可.
,然后利用比例性质求出x即可;(2)先画树状图展示所有12种等可能的结果数,再找出两次摸出的都是红球的结果数,然后根据概率公式计算即可.
【考点精析】通过灵活运用列表法与树状图法和概率公式,掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n即可以解答此题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某学校在进行防溺水安全教育活动中,将以下几种在游泳时的注意事项写在纸条上并折好,内容分别是:①互相关心;②互相提醒;③不要相互嬉水;④相互比潜水深度;⑤选择水流湍急的水域;⑥选择有人看护的游泳池.小颖从这6张纸条中随机抽出一张,抽到内容描述正确的纸条的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB= ![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1: ![]() (i为DF与FC的比值),则背水坡CD的坡长为米.
(i为DF与FC的比值),则背水坡CD的坡长为米.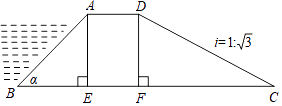
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在直角坐标系内的位置如图所示
(1)分别写出点A,C的坐标:A: ,C: ;
(2)△ABC的周长为 ,面积为 ;
(3)请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC= ![]() ,DE=3.
,DE=3.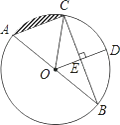
求:
(1)⊙O的半径;
(2)弦AC的长;
(3)阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连接AG,点E、F分别在AG上,连接BE、DF,∠1=∠2,∠3=∠4. 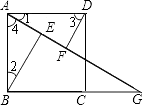
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小学时候大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中a+b的值为( )

A. ﹣6或﹣3 B. ﹣8或1 C. ﹣1或﹣4 D. 1或﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com