
【题目】已知等腰![]() 内接于半径为5的
内接于半径为5的![]() ,已知圆心
,已知圆心![]() 到
到![]() 的距离为3,则这个等腰
的距离为3,则这个等腰![]() 中底边上的高可能是_________.
中底边上的高可能是_________.
【答案】8或2或![]() .
.
【解析】
分四种情况讨论:![]() 是底边,△ABC是锐角三角形、钝角三角形;
是底边,△ABC是锐角三角形、钝角三角形;![]() 是腰,△ABC是锐角三角形、钝角三角形;再分别利用勾股定理和垂径定理求解即可.
是腰,△ABC是锐角三角形、钝角三角形;再分别利用勾股定理和垂径定理求解即可.
解:分情况讨论:
①当![]() 是底边,△ABC是锐角三角形时,连接
是底边,△ABC是锐角三角形时,连接![]() 并延长到
并延长到![]() 于点
于点![]() ,如图1,
,如图1,
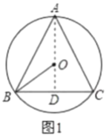
∵![]() ,
,![]() 为外心,
为外心,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
②当![]() 是底边,△ABC是钝角三角形时,连接
是底边,△ABC是钝角三角形时,连接![]() 交
交![]() 于点
于点![]() ,如图2所示,
,如图2所示,
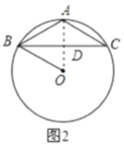
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
③当![]() 是腰,△ABC是锐角三角形时,连接
是腰,△ABC是锐角三角形时,连接![]() 并延长到
并延长到![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,如图3所示,
,如图3所示,
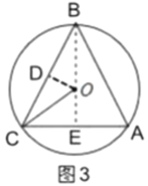
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,在
,在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,解得:
,解得:![]() ,∴
,∴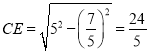 ,
,![]() ,
,
④当![]() 是腰时,△ABC是钝角三角形时,连接
是腰时,△ABC是钝角三角形时,连接![]() 交
交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,如图4所示,
,如图4所示,
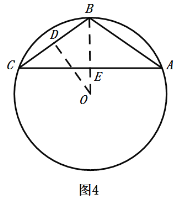
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵△ABC是钝角三角形,即∠ABC>90![]() ,
,
∴∠ABE=∠CBE>45![]() ,
,
∴∠CBE>∠BOD,
∴OD>BD,
而OD=3![]() BD=4,
BD=4,
∴当![]() 是腰,△ABC是钝角三角形,这种情况不存在;
是腰,△ABC是钝角三角形,这种情况不存在;
故答案为:8或2或![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
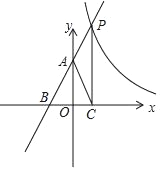
【题目】已知,如图所示直线y=kx+2(k≠0)与反比例函数y=![]() (m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=
(m≠0)分别交于点P,与y轴、x轴分别交于点A和点B,且cos∠ABO=![]() ,过P点作x轴的垂线交于点C,连接AC,
,过P点作x轴的垂线交于点C,连接AC,
(1)求一次函数的解析式.
(2)若AC是△PCB的中线,求反比例函数的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
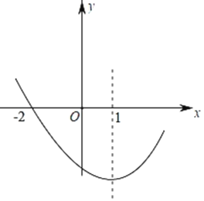
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直x=1线,下列结论中:①abc>0;②若A(x1,m),B(x2,m)是抛物线上的两点,当x=x1+x2时,y=c;③若方程a(x+2)(4﹣x)=﹣2的两根为x1,x2,且x1<x2,则﹣2<x1<x2<4;④(a+c)2>b2;一定正确的是______(填序号即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组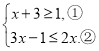
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_____________;
(Ⅱ)解不等式②,得________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
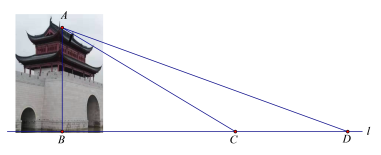
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,线段![]() 及一定点
及一定点![]() ,
,![]() 是线段
是线段![]() 上一动点(
上一动点(![]() 、
、![]() 除外),作直线
除外),作直线![]() ,使
,使![]() 于点
于点![]() ,作直线
,作直线![]() ,使
,使![]() 于点
于点![]() .已知
.已知![]() ,
,![]() ,设
,设![]() ,
,![]() ,数学学习小组根据学习函数的经验,对
,数学学习小组根据学习函数的经验,对![]() 与
与![]() 之间的内在关系进行探究.
之间的内在关系进行探究.
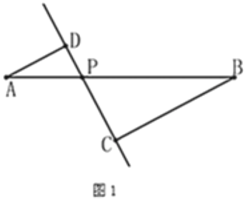
(1)写出y与![]() 之间的关系和
之间的关系和![]() 的取值范围;
的取值范围;
活动操作:
(2)①列表,根据(1)的所求函数关系式讲算并补全表格
| 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
|
| 1.8 | 9 | 21 |
②描点:根据表格中数值,继续在图2中描出剩余的三个点![]() ;
;
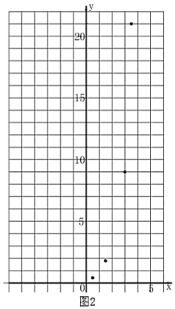
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
数学思考:
(3)请你结合函数的图象,写出该函数的一条性质或结论.
(4)将该函数图象向上移3个单位,再向左平移4个单位后,直接写出平移后的函数关系式和![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得______________________;
(Ⅱ)解不等式②,得____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如图不完整统计图.请结合图中信息,解决下列问题.
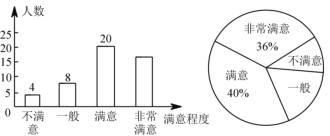
(1)此次调查中接受调查的人数为______人,其中“非常满意”的人数为______人;“一般”部分所在扇形统计图的圆心角度数为_______.
(2)兴趣小组准备从“不满意”的![]() 位群众中随机选择
位群众中随机选择![]() 位进行回访,已知这
位进行回访,已知这![]() 位群众中有
位群众中有![]() 位来自甲片区,另
位来自甲片区,另![]() 位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
位来自乙片区,请用画树状图或列表的方法求出选择的群众都来自甲片区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com