
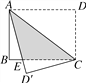
【题目】如图,长方形纸片ABCD沿对角线AC折叠,设点D落在D′处,BC交AD′于点E,AB=6cm,BC=8cm,求阴影部分的面积.
【答案】![]() cm2.
cm2.
【解析】
【试题分析】
因为四边形ABCD是长方形,根据矩形的性质得:∠B=∠D=90°,AB=CD.由折叠的性质可知∠DAC=∠EAC,因为AD//BC,根据平行线的性质,得∠DAC=∠ECA,根据等量代换得,∠EAC=∠ECA,根据等角对等边,得AE=CE.设AE=xcm,在Rt△ABE中,利用勾股定理得,AB2+BE2=AE2,即62+(8-x)2=x2,解得x=![]() ,∴CE=AE=
,∴CE=AE=![]() cm.∴S阴影=
cm.∴S阴影=![]() ·CE·AB=
·CE·AB=![]() ×
×![]() ×6=
×6=![]() (cm2).
(cm2).
【试题解析】
∵四边形ABCD是长方形,∴∠B=∠D=90°,AB=CD.
由折叠的性质可知可知∠DAC=∠EAC,∵AD//BC,
∴∠DAC=∠ECA,∴∠EAC=∠ECA,∴AE=CE.
设AE=xcm,在Rt△ABE中,AB2+BE2=AE2,即62+(8-x)2=x2,∴x=![]() ,∴CE=AE=
,∴CE=AE=![]() cm.∴S阴影=
cm.∴S阴影=![]() ·CE·AB=
·CE·AB=![]() ×
×![]() ×6=
×6=![]() (cm2).故答案为
(cm2).故答案为![]() cm2.
cm2.


科目:初中数学 来源: 题型:
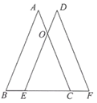
【题目】如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.
(1)求证:△OEC为等腰三角形;
(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
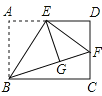
【题目】如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F,若AB=6,BC=![]() ,则CF的长为_______
,则CF的长为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)(1)【问题发现】小明遇到这样一个问题:
如图1,△ABC是等边三角形,点D为BC的中点,且满足∠ADE=60°,DE交等边三角形外角平分线CE所在直线于点E,试探究AD与DE的数量关系.
(1)小明发现,过点D作DF//AC,交AC于点F,通过构造全等三角形,经过推理论证,能够使问题得到解决,请直接写出AD与DE的数量关系: ;
(2)【类比探究】如图2,当点D是线段BC上(除B,C外)任意一点时(其它条件
不变),试猜想AD与DE之间的数量关系,并证明你的结论.
(3)【拓展应用】当点D在线段BC的延长线上,且满足CD=BC(其它条件不变)时,
请直接写出△ABC与△ADE的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB交x轴于点B(6,0),交y轴于点C(0,6),直线AB与直线OA:y=![]() x相交于点A,动点M在线段OA和射线AC上运动.
x相交于点A,动点M在线段OA和射线AC上运动.
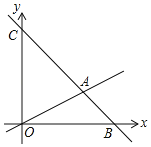
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)是否存在点M,使△OMC的面积是△OAC的面积的![]() ?若存在求出此时点M的坐标;若不存在,说明理由.
?若存在求出此时点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3.
(1)写出它的顶点坐标;
(2)当x取何值时,y随x的增大而增大;
(3)求出图象与x轴的交点坐标.
(4)当x取何值时y的值大于0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小刚两兄弟的家离学校的距离是5km,一天,两兄弟同时从家里出发到学校,小刚以匀速跑步到学校;小明骑自行车出发,骑行一段路程后,因自行车故障,修车耽误了一些时间,然后以比出发时更快的速度赶往学校,结果比小刚早一点到了学校.下列能正确反映两人离家的距离y(千米)与时间t(时)之间的函数关系的图象是( )
A.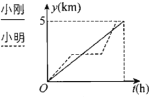 B.
B.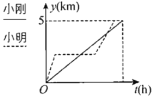
C.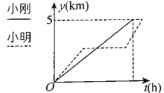 D.
D.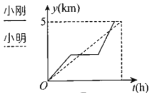
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲村至乙村的公路上有一块山地正在开发,现有一![]() 处需要爆破.已知点
处需要爆破.已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为300米,与公路上的另一停靠站
的距离为300米,与公路上的另一停靠站![]() 的距离为400米,且
的距离为400米,且![]() ,如图所示为了安全起见,爆破点
,如图所示为了安全起见,爆破点![]() 周围半径250米范围内不得进入,问在进行爆破时,公路
周围半径250米范围内不得进入,问在进行爆破时,公路![]() 段是否因为有危险而需要暂时封锁?请说明理由.
段是否因为有危险而需要暂时封锁?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com