
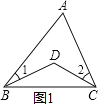
【题目】(1)如图(1),在△ABC中,∠A=62°,∠ABD=20°,∠ACD=35°,求∠BDC的度数.

(2)图(1)所示的图形中,有点像我们常见的学习用品--圆规.我们不妨把这样图形叫做“规形图”,观察“规形图”图(2),试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由.
(3)请你直接利用以上结论,解决以下问题:
①如图(3),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=42°,则∠ABX+∠ACX= °.
②如图(4),DC平分∠ADB,EC平分∠AEB,若∠DAE=60°,∠DBE=140°,求∠DCE的度数.
③如图(5),∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG1C=68°,求∠A的度数.
【答案】(1)117°;(2)∠BDC=∠A+∠B+∠C;;(3)①48°;②100°;③60°.
【解析】
(1)先根据三角形内角和定理求出∠ABC+∠ACB的度数,再由∠1=20°,∠2=35°求出∠DBC+∠DCB的度数,由三角形内角和定理即可得出结论;
(2)首先连接AD并延长至点F,然后根据外角的性质,即可判断出∠BDC=∠A+∠B+∠C.
(3)①由(1)可得∠ABX+∠ACX+∠A=∠BXC,然后根据∠A=42°,∠BXC=90°,求出∠ABX+∠ACX的值是多少即可.
②由(1)可得∠DBE=∠DAE+∠ADB+∠AEB,再根据∠DAE=60°,∠DBE=140°,求出∠ADB+∠AEB的值是多少;然后根据∠DCE=![]() (∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
(∠ADB+∠AEB)+∠DAE,求出∠DCE的度数是多少即可.
③根据∠BG1C=![]() (∠ABD+∠ACD)+∠A,∠BG1C=68°,设∠A为x°,可得∠ABD+∠ACD=140°-x°,解方程,求出x的值,即可判断出∠A的度数是多少.
(∠ABD+∠ACD)+∠A,∠BG1C=68°,设∠A为x°,可得∠ABD+∠ACD=140°-x°,解方程,求出x的值,即可判断出∠A的度数是多少.
(1)∵在△ABC中,∠A=62°,
∴∠ABC+∠ACB=180°-62°=118°.
∵∠1=20°,∠2=35°,
∴∠DBC+∠DCB=∠ABC+∠ACB-∠1-∠2=118°-20°-35°=63°.
∴∠BDC=180°-(∠DBC+∠DCB)=180°-63°=117°;
(2)如图2,连接AD并延长至点F,
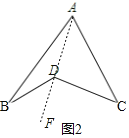
根据外角的性质,可得
∠BDF=∠BAD+∠B,∠CDF=∠C+∠CAD,
又∵∠BDC=∠BDF+∠CDF,∠BAC=∠BAD+∠CAD,
∴∠BDC=∠A+∠B+∠C;
(3)①由(1),可得
∠ABX+∠ACX+∠A=∠BXC,
∵∠A=42°,∠BXC=90°,
∴∠ABX+∠ACX=90°-42°=48°;
故答案为:48°;
②由(1),可得
∠DBE=∠DAE+∠ADB+∠AEB,
∴∠ADB+∠AEB=∠DBE-∠DAE=140°-60°=80°,
∴![]() (∠ADB+∠AEB)=80°÷2=40°,
(∠ADB+∠AEB)=80°÷2=40°,
∴∠DCE=![]() (∠ADB+∠AEB)+∠DAE
(∠ADB+∠AEB)+∠DAE
=40°+60°
=100°;
③∠BG1C=![]() (∠ABD+∠ACD)+∠A,
(∠ABD+∠ACD)+∠A,
∵∠BG1C=68°,
∴设∠A为x°,
∵∠ABD+∠ACD=140°-x°
∴![]() (140-x)+x=70,
(140-x)+x=70,
∴14-![]() x+x=68,
x+x=68,
解得x=60
即∠A的度数为60°.


科目:初中数学 来源: 题型:
【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.
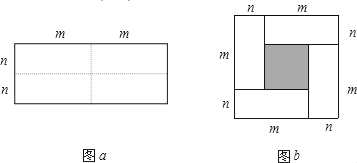
(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个装有2个红球和3个白球(每个球除颜色外完全相同)的盒子中任意摸出一个球,摸到红球小明获胜,摸到白球小刚获胜,这个游戏对双方公平吗?为什么?如何修改可以让游戏公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与x轴有交点.
与x轴有交点.
(1)求m的取值范围;
(2)如果该二次函数的图像与x轴的交点分别为(x1,0),(x2,0),且2 x1 x2+ x1+ x2≥20,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
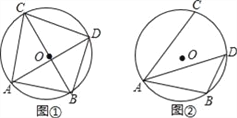
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.
观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>![]() 的解集.
的解集.
有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.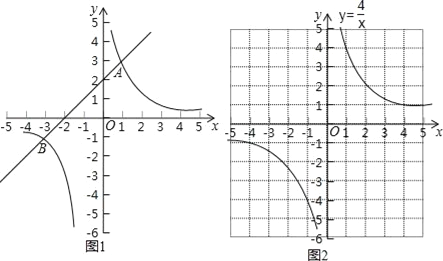
下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>![]() ;
;
当x<0时,原不等式可以转化为x2+4x﹣1<![]() ;
;
(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[-2.5]=-3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<-1.5>=-1.解决下列问题:
(1)[-2.6]=______,<6.2>=______.
(2)已知x,y满足方程组 ,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
,则[x]=______,<y>=______,x的取值范围是______,y的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
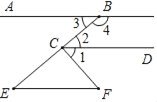
【题目】把下面的推理过程补充完整,并在括号内填上理由.
已知:B、C、E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
试说明:∠BCF=∠E+∠F
解:∵∠3=∠E(已知)
∴EF∥ (内错角相等,两直线平行)
∵∠4+∠2=180°(已知)
∴CD∥
∴CD∥ (平行于同一条直线的两条直线互相平行)
∴∠1=∠F,
∠2=
∵∠BCF=∠1+∠2(已知)
∴∠BCF=∠E+∠F(等量代换)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com