
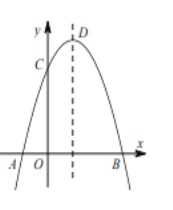
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和
和![]() ,交
,交![]() 轴于点
轴于点![]() 抛物线的顶点为
抛物线的顶点为![]() ,下列四个结论:
,下列四个结论:
①点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 时,
时,![]() 是等腰直角三角形;
是等腰直角三角形;
③若![]() ,则
,则![]()
④抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]()
其中结论正确的序号是__________.
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】为助力我省脱贫攻坚,某村在“农村淘宝网店”上销售该村优质农产品,该网店于今年六月底收购一批农产品,七月份销售![]() 袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到
袋,八、九月该商品十分畅销,销售量持续走高,在售价不变的基础上,九月份的销售量达到![]() 袋.
袋.
(1)求八、九这两个月销售量的月平均增长率;
(2)该网店十月降价促销,经调查发现,若该农产品每袋降价![]() 元,销售量可增加
元,销售量可增加![]() 袋,当农产品每袋降价多少元时,这种农产品在十月份可获利
袋,当农产品每袋降价多少元时,这种农产品在十月份可获利![]() 元?(若农产品每袋进价
元?(若农产品每袋进价![]() 元,原售价为每袋
元,原售价为每袋![]() 元)
元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在一张ABCD的纸片中,ABCD的面积为6,DC=3,∠BCD=45°,点P是BD上的一动点(点P与点B,D不重合).现将这张纸片分别沿BD,AP剪成三块,并按图2(注:图2中的①,②是将图1中的①,②翻转背面朝上,再拼接而成的)所示放置
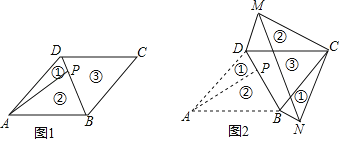
(1)当点P是BD的中点时,求AP的长.
(2)试探究:当点P在BD的什么位置上时,MN的长最小?请求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上,如图2,△ABC以点A为旋转中心顺时针旋转.
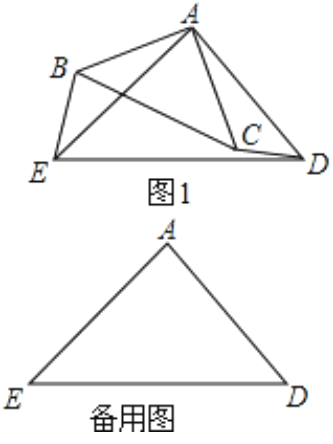
(1)证明:BE=CD
(2)当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的旋转角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,求出角α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
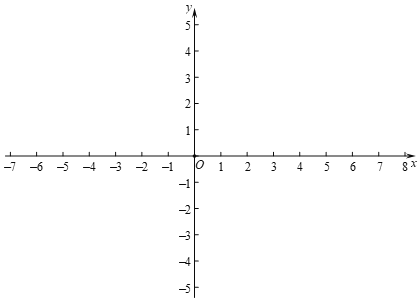
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两盒中分别标注数字2、![]() 、
、![]() 、和
、和![]() 、1、6的3张卡片,这些卡片除数字外都相同,把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把从甲盒中抽得卡片上的数字作为一个点的横坐标,从乙盒中抽得卡片上的数字作为这个点的纵坐标.
、1、6的3张卡片,这些卡片除数字外都相同,把卡片洗匀后,从甲、乙两盒中各任意抽取1张,并把从甲盒中抽得卡片上的数字作为一个点的横坐标,从乙盒中抽得卡片上的数字作为这个点的纵坐标.
(1)请利用列表或画树状图的方法列出这样的点所有可能的坐标;
(2)计算这些点落在以原点为圆心、3为半径的圆内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件。
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?
(2)若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com