
| A. | 300° | B. | 240° | C. | 180° | D. | 120° |
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).
如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1,B2,B3,…,则B2015的坐标为(1342.5,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
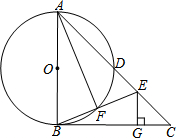 如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.
如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,∠BAC=2∠CBE,交AC于点E,交⊙O于点F,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
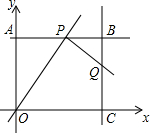 如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
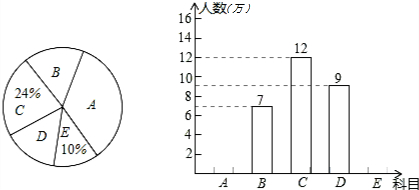 园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).
园;D:明月岛,E:青年林场.市旅游局对某月进入景点的人数情况进行调查统计,制成了两幅不完整的统计图(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com