
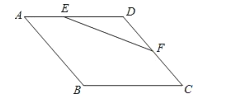
【题目】如图,菱形![]() 的边长为
的边长为![]() ,
,![]() ,点
,点![]() 是
是![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),点
重合),点![]() 是
是![]() 上一动点,且
上一动点,且![]() ,则
,则![]() 面积的最大值为__________.
面积的最大值为__________.
【答案】![]()
【解析】
首先过点F作FG⊥AD,交AD的延长线于点G,由菱形ABCD的边长为4,∠BAD=60°,即可求得AD=CD=4,∠FDG=60°,然后设AE=x,即可得S△DEF=![]() DEFG)=-
DEFG)=-![]() (x-2)2+
(x-2)2+![]() ,然后根据二次函数的性质,即可求得答案.
,然后根据二次函数的性质,即可求得答案.
解:过点F作FG⊥AD,交AD的延长线于点G,
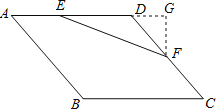
∵菱形ABCD边长为4,∠BAD=60°,
∴AD=CD=4,∠ADC=180°-∠BAD=120°,
∴∠FDG=180°-∠ADB=60°,
设AE=x,
∵AE+CF=4,
∴CF=4-x;
∴DE=AD-AE=4-x,DF=CD-CF=4-(4-x)=x,
在Rt△DFG中,FG=DFsin∠GDF=![]() x,
x,
∴S△DEF=![]() DEFG=
DEFG=![]() ×(4-x)×
×(4-x)×![]() x=-
x=-![]() x2+
x2+![]() x=-
x=-![]() (x2-4x)=-
(x2-4x)=-![]() (x-2)2+
(x-2)2+![]() ,
,
∴当x=2时,△DEF面积的最大,最大值为![]() .
.
故答案为:![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于5的关联数,求
是关于5的关联数,求![]() 的值
的值
(2)若![]() 与
与![]() 是关于4的关联数,求
是关于4的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
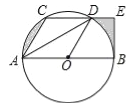
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线l,y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,﹣3).
(1)求抛物线l的顶点P的坐标为的A的坐标;
(2)将抛物线l先向上平移3个单位长度,再向左平移2个单位长度,得到抛物线l1,请直接写出平移后的抛物线l1的表达式;
(3)将抛物线l向右平移m个单位长度,得到抛物线l2,其中点A的对应点为点M,若点M、A、P是恰好一个矩形的三个顶点,请求出m的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
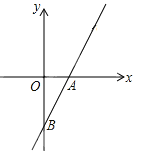
(1)求直线AB的解析式;
(2)直线AB上是否存在点C,使△BOC的面积为2?若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
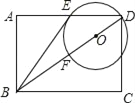
【题目】已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.
(1)判断直线BE与⊙O的位置关系,并证明你的结论;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P(x,y),请用“列表法”或“树状图法”求点P(x,y)在函数y=-x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年底,2020年初我国爆发了新冠肺炎疫情,为了增加学生对疫情和肺炎的预防知识的了解,某学校利用网络开展了相关知识的宣传教育活动,为了解这次的宣传效果,学校从全校3600名学生中随机抽取200名学生进行知识测试(满分100分,得分均为整数),并根据这200人的测试成绩,制订如下统计图表:

(1) ![]() ,
,![]() ,成绩最好的等级A所占的百分比;
,成绩最好的等级A所占的百分比;
(2)张亮在这次测试中成绩为85分,你认为85分一定是这200名学生知识测试成绩的中位数吗?请简要说明理由;
(3)如果80分以上(包括80分)为优秀,请估计全校3600名学生中成绩优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止.过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5秒时,PD的长是( )
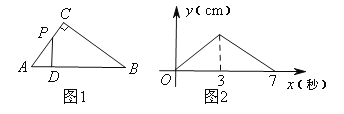
A.1.5cmB.1.2cmC.1.8cmD.2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com