
科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表).
温度x/℃…-4-20244.5…植物每天高度
增长量y/mm…414949412519.75…由这些数据,科学家推测出植物每天高度增长量y是温度x的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度增长最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250 mm,那么实验室的温度x应该在哪个范围内选择?直接写出结果.
(1)选择二次函数,因为当x=0时,y=49,所以c=49.所以设y=ax2+bx+49,得
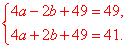 解得
解得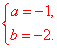
∴y关于x的函数关系式是y=-x2-2x+49.
不选另外两个函数的理由:
∵点(0,49)不可能在反比例函数图象上,
∴y不是x的反比例函数;
∵点(-4,41),(-2,49),(2,41)不在同一直线上,∴y不是x的一次函数.
(2)由(1),得y=-x2-2x+49=-(x+1)2+50.
∵a=-1<0,∴当x=-1时,y有最大值为50,
即当温度为-1 ℃时,这种植物每天高度增长量最大.
(3)∵10天内要使该植物高度增长量的总和超过250 mm,
∴平均每天该植物高度增长量超过25 mm,
当y=25时,-x2-2x+49=25,
整理,得x2+2x-24=0,解得x1=-6,x2=4,
∴在10天内要使该植物高度增长量的总和超过250 mm,实验室的温度应保持在-6 ℃<x<4 ℃.


科目:初中数学 来源: 题型:
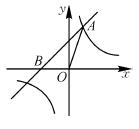
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
(1)求k和b的值.
(2)求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
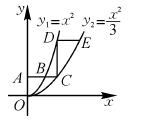
如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=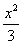 (x≥0)的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于E,则
(x≥0)的图象于B,C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于E,则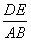 = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种10棵橘子树,橘子总个数最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
株洲五桥主桥主孔为拱梁钢构组合体系如图1,小明在五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,将余下的8根支柱的高度都算出来了,你认为中柱右边第二根支柱的高度是( )
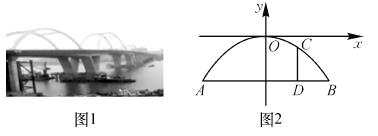
A.7米 B.7.6米 C.8米 D.8.4米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:解答题
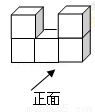
(4分)5个棱长为1的正方体组成如图所示的几何体,画出该几何体从正面和左面看到的图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一座桥,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24 m,最高点离水面8 m,以水平线AB为x轴,AB的中点为原点建立坐标系.
(1)求此桥拱线所在抛物线的解析式;
(2)桥边有一艘船,浮在水面部分高4 m,最宽处12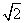 m,试探索此船能否开到桥下?说明理由.
m,试探索此船能否开到桥下?说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省九年级下学期期始考试数学试卷(解析版) 题型:解答题
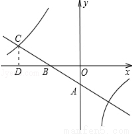
(本题10分)如图,一次函数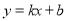 的图象与坐标轴分别交于A、B两点,与反比例函数
的图象与坐标轴分别交于A、B两点,与反比例函数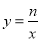 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的表达式;
(2)直接写出当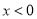 时,
时,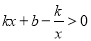 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com