
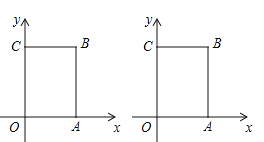
����Ŀ����ͼ���ڳ�����OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬��A������Ϊ��a��0������C������Ϊ��0��b����a��b����![]() +|b��6|��0����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��C��B��A��O����·�ƶ���
+|b��6|��0����B�ڵ�һ�����ڣ���P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��C��B��A��O����·�ƶ���
��1����B������Ϊ�� ��������P�ƶ�3.5��ʱ����P������Ϊ�� ����
��2�����ƶ������У�����P��x��ľ���Ϊ4����λ����ʱ�����P�ƶ���ʱ�䣻
��3����O��C��B����·�ƶ������У��Ƿ���ڵ�Pʹ��OBP�������10�������������P�ƶ���ʱ�䣻�������ڣ���˵�����ɣ�
���𰸡���1����4,6������1,6������2��2���6�룻��3��![]() ��
��![]() .
.
��������
��1�����÷Ǹ��������ʿ������a��b��ֵ�����ݳ����ε����ʣ�������õ�B�����ꣻ���������P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-C-B-A-O����·�ƶ������Եõ�����P�ƶ�4��ʱ����P��λ�ú͵�P�����ꣻ
��2����������Եõ�����Ҫ���������������ֱ������������µ�P�ƶ���ʱ�伴�ɣ�
��3����Ϊ��P��OC��BC�Ϸ�����㼴�ɣ�
��1����a��b����![]() +|b-6|=0��
+|b-6|=0��
��a-4=0��b-6=0��
���a=4��b=6��
���B�������ǣ�4��6����
�ߵ�P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-C-B-A-O����·�ƶ���
��2��3.5=7��
��OA=4��OC=6��
�൱��P�ƶ�4��ʱ�����߶�CB�ϣ����C�ľ����ǣ�7-6=1��
������P�ƶ�4��ʱ����ʱ��P���߶�CB�ϣ����C�ľ�����2����λ���ȣ���P�������ǣ�1��6����
�ʴ�Ϊ��4��6������1��6����
��2��������ɵã����ƶ������У�����P��x��ľ���Ϊ4����λ����ʱ���������������
��һ�����������P��OC��ʱ��
��P�ƶ���ʱ���ǣ�4��2=2�룬
�ڶ������������P��BA��ʱ��
��P�ƶ���ʱ���ǣ���6+4+2����2=6�룬
�����ƶ������У�����P��x��ľ���Ϊ4����λ����ʱ����P�ƶ���ʱ����2���6�룮
��3����ͼ1��ʾ��
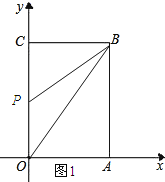
�ߡ�OBP�����=10��
��![]() OPBC=10����
OPBC=10����![]() ��4��OP=10��
��4��OP=10��
��ã�OP=5��
���ʱt=2.5s
��ͼ2��ʾ��
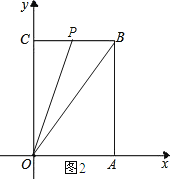
�ߡ�OBP�����=10��
��![]() PBOC=10����
PBOC=10���� ![]() ��6��PB=10��
��6��PB=10��
��ã�BP=![]() ��
��
��CP=![]() ��
��
��OC+CP=6+![]() =
=![]() ��
��
���ʱt=![]() s��
s��
��������������������ʱ��t��ֵΪ2.5s��![]() s��
s��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
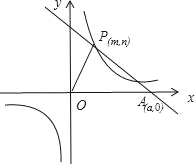
����Ŀ����֪��O������ԭ�㣬P��m��n����m��0���Ǻ���y=![]() ��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m��������OPA�����Ϊs����s=1+
��k��0���ϵĵ㣬����P��ֱ��PA��OP��P��ֱ��PA��x��������ύ�ڵ�A��a��0����a��m��������OPA�����Ϊs����s=1+![]() ��
��
��1����n=1ʱ�����A�����ꣻ
��2����OP=AP����k��ֵ��
��3����n��С��20����������k��![]() ����OP2����Сֵ��
����OP2����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬ�ľ��ο�Ƭ������ͼ��ʽ�ڷ���һ��ֱ���ϣ�ÿ�����ο�Ƭ��Ϊ2����Ϊ1���������ƣ��ڷ�2014��ʱ��ʵ�߲��ֳ�Ϊ_____��
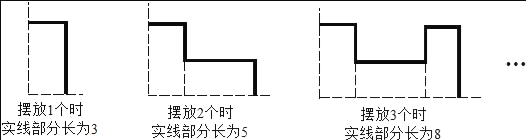
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��DF=BE��

��1����֤��CE=CF��
��2������G��AD�ϣ�����GCE=45������GE=BE+GD������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������Ǻ���y��![]() (mΪ����)ͼ���һ֧��
(mΪ����)ͼ���һ֧��
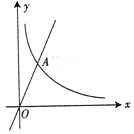
(1)����m��ȡֵ��Χ��
(2)���ú�����ͼ��������������y��2x��ͼ���ڵ�һ���Ľ���ΪA(2��n)�����A�����꼰������
�����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ�ѡ���У�����y����x�ĺ������ǣ� ��
A��|y|=x��1 B��y=![]() C��y=2x��7 D��y=x2
C��y=2x��7 D��y=x2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������֦Ǧ�ʷָ��ס��������༶���װ���һ�˷ֵ�6֦�������ÿ�˶��ֵ�13֦���Ұ���һ�˷ֵ�5֦�������ÿ�˶��ֵ�10֦.����ֵ������༶��Ǧ����Ŀ��ͬ�����Ҵ���100��������200��ô�ס�����������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�������������ͼ��
��1��д���ü���������ƣ���������ʾ���ݼ������������ı������
��2�����һֻ����Ҫ������������еĵ�B�������ر�������AC���е�D��������������·�����·�̣�
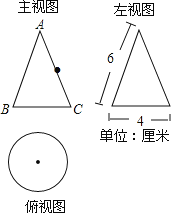
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������һ��̨��������ɼн�Ϊ30������̨��͵�A����ߵ�B�ľ���Ϊ10![]() ��A��B������ǰ���д�ֱ�ڵ�������DE����A��B���㴦������������˶���E�����Ƿֱ�Ϊ60����15�������Ǽ�������ˮƽ�ߵļнǣ�
��A��B������ǰ���д�ֱ�ڵ�������DE����A��B���㴦������������˶���E�����Ƿֱ�Ϊ60����15�������Ǽ�������ˮƽ�ߵļнǣ�
��1����AE�ij���
��2����֪�������һ���������1��F�㴦����������0.5��/����ٶ������������������쵽����˶�����Ҫ�����룿
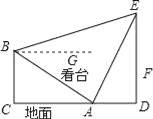
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com