
【题目】已知:在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() 的垂线与过点
的垂线与过点![]() 的直线交于
的直线交于![]() 、
、![]() 两点.
两点.
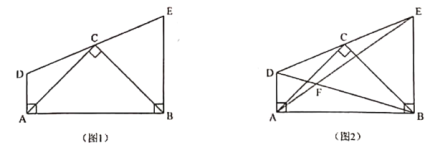
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 、
、![]() 相交于点
相交于点![]() ,在不添加任何辅助线的情况下,请写出图2中的四对三角形,使写出的每对三角形面积相等.
,在不添加任何辅助线的情况下,请写出图2中的四对三角形,使写出的每对三角形面积相等.
【答案】(1)详见解析;(2)详见解析.
【解析】
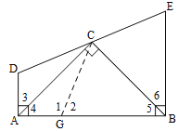
(1)在AB上截取AG=AD,通过证明△ADC≌△AGC,可得∠D=∠1,由补角的性质可得∠2=∠E,通过证明△BCG≌△BCE,可得BG=BE,即可得结论;
(2)由等底等高的两个三角形面积相等和三角形中线性质可求解.
(1)证明:在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,
∵![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() (SAS),
(SAS),
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() (AAS),
(AAS),
∴![]() ,
,
∴![]() ;
;
(2))∵AD∥BE,
∴S△EAD=S△BAD,S△ABE=S△DEB,
∴S△EDF=S△FAB,
由(1)可知,DC=CE=CG,
∴S△BCD=S△BCE,
∴△EAD和△BAD,△AEB和△DEB,△FDE和△FAB,△BCE和△BCD,每对三角形面积相等.


科目:初中数学 来源: 题型:
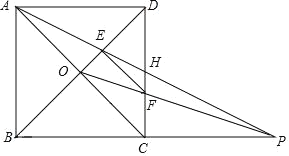
【题目】如图,正方形ABCD的边长为1.对角线AC、BD相交于点O,P是BC延长线上的一点,AP交BD于点E,交CD于点H,OP交CD于点F,且EF与AC平行.
(1)求证:EF⊥BD.
(2)求证:四边形ACPD为平行四边形.
(3)求OF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(与点
上的动点(与点![]() 不重合),连接
不重合),连接![]() .
.
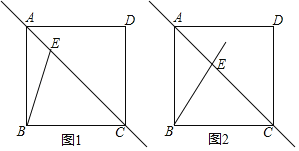
(1)将射线![]() 绕点
绕点![]() 顺时针旋转45°,交直线
顺时针旋转45°,交直线![]() 于点
于点![]() .
.
①依题意补全图1;
②小研通过观察、实验,发现线段![]() ,
,![]() ,
,![]() 存在以下数量关系:
存在以下数量关系:
![]() 与
与![]() 的平方和等于
的平方和等于![]() 的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:
想法1:将线段![]() 绕点
绕点![]() 逆时针旋转90°,得到线段
逆时针旋转90°,得到线段![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
想法2:将![]() 沿
沿![]() 翻折,得到
翻折,得到![]() ,要证
,要证![]() 的关系,只需证
的关系,只需证![]() 的关系.
的关系.
…
请你参考上面的想法,用等式表示线段![]() 的数量关系并证明;(一种方法即可)
的数量关系并证明;(一种方法即可)
(2)如图2,若将直线![]() 绕点
绕点![]() 顺时针旋转135°,交直线
顺时针旋转135°,交直线![]() 于点
于点![]() .小研完成作图后,发现直线
.小研完成作图后,发现直线![]() 上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
上存在三条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,经过某点且平行于
,经过某点且平行于![]() 、
、![]() 或
或![]() 的直线,叫该点关于
的直线,叫该点关于![]() 的“关联线”.
的“关联线”.
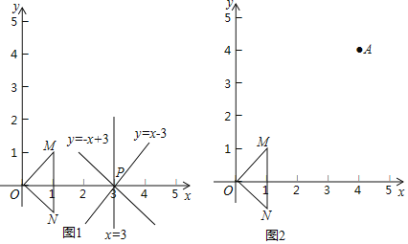
例如,如图1,点![]() 关于
关于![]() 的“关联线”是:
的“关联线”是:![]() ,
,![]() ,
,![]() .
.
(1)在以下3条线中,________是点![]() 关于
关于![]() 的“关联线”(填出所有正确的序号);①
的“关联线”(填出所有正确的序号);①![]() ;②
;②![]() ;③
;③![]() .
.
(2)如图2,抛物线![]() 经过点
经过点![]() ,顶点
,顶点![]() 在第一象限,且
在第一象限,且![]() 点有一条关于
点有一条关于![]() 的“关联线”是
的“关联线”是![]() ,求此抛物线的表达式;
,求此抛物线的表达式;
(3)在(2)的条件下,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是线段
是线段![]() 上除点
上除点![]() 外的任意一点,连接
外的任意一点,连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 的位置,当点
的位置,当点![]() 在
在![]() 点关于
点关于![]() 的平行于
的平行于![]() 的“关联线”上时,满足(2)中条件的抛物线沿对称轴向下平移多少距离,其顶点落在
的“关联线”上时,满足(2)中条件的抛物线沿对称轴向下平移多少距离,其顶点落在![]() 上?
上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+2ax﹣3a(a>0)与x轴交于A,B两点(点A在点B的左侧).
(1)求抛物线的对称轴及线段AB的长;
(2)抛物线的顶点为P,若∠APB=120°,求顶点P的坐标及a的值;
(3)若在抛物线上存在一点N,使得∠ANB=90°,结合图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
, ![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙ O 的半径是![]() ,
,

①求出⊙ O 上的所有梦之点的坐标;
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,tan∠OAQ= 1.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面数据是截至2010年费尔兹奖得主获奖时的年龄:
29 39 35 33 39 28 33 35 31 31 37 32 38
36 31 39 32 38 37 34 29 34 38 32 35 36
33 29 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 40 31 38 38 40 40 37
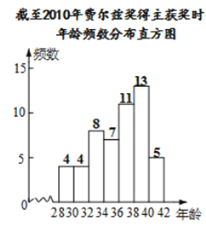
小果、小冻、小甜将数据整理,分别按组距是2,5,10进行分组,列出频数分布表,画出频数分布直方图,如下:
年龄 | 频数 |
| 4 |
| 4 |
| 8 |
| 7 |
| 11 |
| 13 |
| 5 |
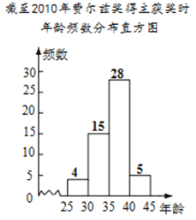
年龄 | 频数 |
| 4 |
| 15 |
| 28 |
| 5 |
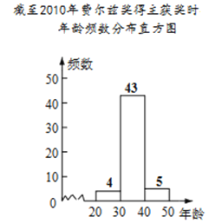
年龄 | 频数 |
| 4 |
| 43 |
| 5 |
根据以上材料回答问题:
小果、小冻、小甜三人中,比较哪一位同学分组能更好的说明费尔兹奖得主获奖时的年龄分布,并简要说明其他两位同学分组的不足之处.

费尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,主要授予年轻的数学家,美籍华人丘成桐(1949年出生)1982年获费尔兹奖.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据《太原市电动自行车管理条例》的规定,2019年5月1日起,未上牌的电动自行车将禁止上路行驶,而电动自行车上牌登记必须满足国家标准.某商店购进了甲.乙两种符合国家标准的新款电动自行车.其中甲种车总进价为22500元,乙种车总进价为45000元,已知乙种车每辆的进价是甲种车进价的1.5倍,且购进的甲种车比乙种车少5辆.
(1)甲种电动自行车每辆的进价是多少元?
(2)这批电动自行车上市后很快销售一空.该商店计划按原进价再次购进这两种电动自行车共50辆,将新购进的电动自行车按照表格中的售价销售.设新购进甲种车m辆(20≤m≤30),两种车全部售出的总利润为y元(不计其他成本).
①求y与m之间的函数关系式;
②商店怎样安排进货方案,才能使销售完这批电动自行车获得的利润最大?最大利润是多少?
型号 | 甲 | 乙 |
售价(元/辆) | 2000 | 2800 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com