
【题目】如图,在矩形ABCD中,E,F分别是AD,CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD= . 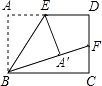
【答案】2 ![]()
【解析】解:如图,连接EF,
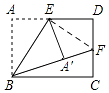
∵点E、点F是AD、DC的中点,
∴AE=ED,CF=DF= ![]() CD=
CD= ![]() AB=1,
AB=1,
由折叠的性质可得AE=A′E,
∴A′E=DE,
在Rt△EA′F和Rt△EDF中,
![]() ,
,
∴Rt△EA′F≌Rt△EDF(HL),
∴A′F=DF=1,
∴BF=BA′+A′F=AB+DF=2+1=3,
在Rt△BCF中,
BC= ![]() =
= ![]() =2
=2 ![]() .
.
∴AD=BC=2 ![]() .
.
故答案为:2 ![]() .
.
连接EF,由中点定义∴AE=ED,CF=DF=1,由折叠的性质可得AE=A′E,故A′E=DE,由HL证出Rt△EA′F≌Rt△EDF由全等三角形的性质得A′F=DF=1,BF=BA′+A′F=AB+DF=2+1=3,由勾股定理得BC得长度进而得出结论。


科目:初中数学 来源: 题型:
【题目】某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: ![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73.)
≈1.73.)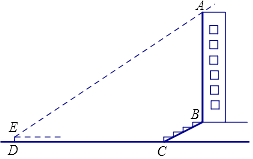
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨,某物流公司现有26吨货物,计划A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发以每秒2cm的速度沿A→C→B运动,设点P运动的时间是t秒,那么当t=____,△APE的面积等于6.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD.
(1)作图,作∠A的平分线AE交CD于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断△AED的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC内有一个点P1,当P1、A、B、C没有任何三点在同一直线上时,如图1,可构成3个互不重叠的小三角形;若△ABC内有两个点P1、P2,其它条件不变,如图2,可构成5个互不重叠的小三角形:……若△ABC内有n个点,其它条件不变,则构成若干个互不重叠的小三角形,这些小三角形的内角和为()
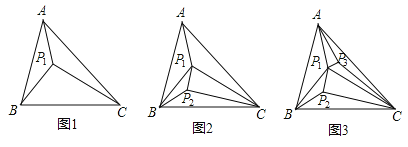
A.n·180°B.(n+2)·180°C.(2n-1)·180°D.(2n+1)·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,纸上有5个边长为1的小正方形组成的纸片.可以用下面的方法把它剪拼成一个正方形.
(1)拼成的正方形的面积是多少,边长是多少.
(2)你能在3×3的正方形方格图3中,连接四个点组成面积为5的正方形吗?
(3)如图4,你能把这十个小正方形组成的图形纸,剪开并拼成一个大正方形吗?若能,请画出示意图,并写出边长为多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com