
【题目】将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF.
(1)如图1,若∠ABC=α=60°,BF=AF.
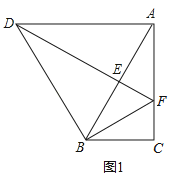
①求证:DA∥BC;②猜想线段DF、AF的数量关系,并证明你的猜想;
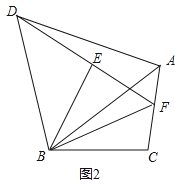
(2)如图2,若∠ABC<α,BF=mAF(m为常数),求![]() 的值(用含m、α的式子表示).
的值(用含m、α的式子表示).
【答案】解:(1)①证明:由旋转性质可知,∠DBE=∠ABC=60°,BD=AB。
∴△ABD为等边三角形。∴∠DAB=60°。∴∠DAB=∠ABC。
∴DA∥BC。
②猜想:DF=2AF。证明如下:
如答图1所示,在DF上截取DG=AF,连接BG,
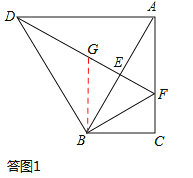
由旋转性质可知,DB=AB,∠BDG=∠BAF,
∵在△DBG与△ABF中,DB=AB,∠BDG=∠BAF,DG=AF,
∴△DBG≌△ABF(SAS)。∴BG=BF,∠DBG=∠ABF。
∵∠DBG+∠GBE=α=60°,∴∠GBE+∠ABF=60°,即∠GBF=α=60°。
又∵BG=BF,∴△BGF为等边三角形。∴GF=BF。
又∵BF=AF,∴GF=AF。∴DF=DG+GF=AF+AF=2AF。
(2)如答图2所示,在DF上截取DG=AF,连接BG,

由(1),同理可证明△DBG≌△ABF,BG=BF,∠GBF=α。
过点B作BN⊥GF于点N,
∵BG=BF,∴点N为GF中点,∠FBN=![]() 。
。
在Rt△BFN中,NF=BFsin∠FBN=BFsin![]() =mAFsin
=mAFsin![]() .
.
∴GF=2NF=2mAFsin![]() 。∴DF=DG+GF=AF+2mAFsin
。∴DF=DG+GF=AF+2mAFsin![]() 。
。
∴![]() 。
。
【解析】
试题分析:(1)由旋转性质证明△ABD为等边三角形,则∠DAB=∠ABC=60°,所以DA∥BC。
(2)①如答图1所示,作辅助线(在DF上截取DG=AF,连接BG),构造全等三角形△DBG≌△ABF,得到BG=BF,∠DBG=∠ABF;进而证明△BGF为等边三角形,则GF=BF=AF;从而DF=2AF。
②与①类似,作辅助线,构造全等三角形△DBG≌△ABF,得到BG=BF,∠DBG=∠ABF,由此可知△BGF为顶角为α的等腰三角形,解直角三角形求出GF的长度,从而得到DF长度,问题得解。


科目:初中数学 来源: 题型:
【题目】(8分)甲,乙,丙三位学生进入了“校园朗诵比赛”冠军、亚军和季军的决赛,他们将通过抽签来决定比赛的出场顺序.
(1)求甲第一个出场的概率;
(2)求甲比乙先出场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.

(1)若自由转动转盘,当它停止转动时,指针指向奇数区的概率是多少?
(2)若自由转动转盘,当它停止转动时,指针指向的数小于或等于4的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
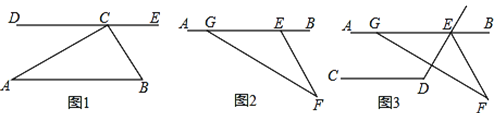
【题目】已知任意三角形ABC,
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 a,b,c 分别是△ABC 的三边长.
(1)分解因式:①ac﹣bc= ,②﹣a2+2ab﹣b2= ;
(2)若 ac﹣bc=﹣a2+2ab﹣b2,试判断△ABC 的形状;并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).

(1)请在网格平面内作出平面直角坐标系;
(2)将△ABC平移至△DEF,使得A、B、C的对应点依次是D、E、F,已知D(2,3),请在网格中作出△DEF;
(3)若Q(a,b)是△DEF内一点,则△ABC内点Q的对应点点P的坐标是 (用a、b表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com