练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，转盘被等分成六个扇形，并在上面依次写上数字1、2、3、4、5、6.

    （1）若自由转动转盘，当它停止转动时，指针指向奇数区的概率是多少？

    （2）若自由转动转盘，当它停止转动时，指针指向的数小于或等于4的概率是多少？

    【答案】（1）；（2）

    【解析】

    （1）先指出指向数字总共的结果，再指出指向奇数区的结果即可；

    （2）先指出指向数字总共的结果，再指出指针指向的数小于或等于4的结果即可.

    解：（1）自由转动转盘，当它停止转动时，指针指向数字的结果总共有6种，指针指向奇数区的结果有3种，所以指针指向奇数区的概率是.

    （2）自由转动转盘，当它停止转动时，指针指向数字的结果总共有6种，指针指向的数小于或等于4的结果有4种，所以指针指向的数不大于4的概率是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同，春节期间，两家采摘园将推出优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的草莓六折优惠；乙园的优惠方案是：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠.优惠期间，某游客的草莓采摘量为（千克），在甲园所需总费用为（元），在乙园所需总费用为（元），、与之间的函数关系如图所示.

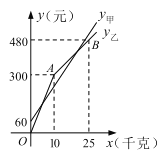
    （1）甲采摘园的门票是_____元，两个采摘园优惠前的草莓单价是每千克____元；

    （2）当时，求与的函数表达式；

    （3）游客在“春节期间”采摘多少千克草莓时，甲、乙两家采摘园的总费用相同.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在将式子（m＞0）化简时，

    小明的方法是：===；

    小亮的方法是： ；

    小丽的方法是：.

    则下列说法正确的是（　　）

    A. 小明、小亮的方法正确，小丽的方法不正确

    B. 小明、小丽的方法正确，小亮的方法不正确

    C. 小明、小亮、小丽的方法都正确

    D. 小明、小丽、小亮的方法都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB=16cm，BC=6cm，点P从点A出发沿AB向点B移动（不与点A、B重合），一直到达点B为止；同时，点Q从点C出发沿CD向点D移动（不与点C、D重合）．运动时间设为t秒．

    （1）若点P、Q均以3cm/s的速度移动，则：AP=　　cm；QC=　　cm．（用含t的代数式表示）

    （2）若点P为3cm/s的速度移动，点Q以2cm/s的速度移动，经过多长时间PD=PQ，使△DPQ为等腰三角形？

    （3）若点P、Q均以3cm/s的速度移动，经过多长时间，四边形BPDQ为菱形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x1，x2是关于x的一元二次方程x2－2(m＋1)x＋m2＋5＝0的两实根．

    (1)若(x1－1)(x2－1)＝28，求m的值；

    (2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．

    【答案】（1）m的值为6;（2）17.

    【解析】试题分析：

    （1）由题意和根与系数的关系可得：x1＋x2＝2(m＋1)，x1x2＝m2＋5；由(x1－1)(x2－1)＝28，可得：x1x2－(x1＋x2)＝27；从而得到：m2＋5－2(m＋1)＝27，解方程求得m的值，再由“一元二次方程根的判别式”进行检验即可得到m的值；

    （2）①当7为腰长时，则方程的两根中有一根为7，代入方程可解得m的值（此时m的取值需满足根的判别式△ ），将m的值代入原方程，可求得两根（此时两根和7需满足三角形三边之间的关系），从而可求得等腰三角形的周长；

    ②当7为底边时，则方程的两根相等，由此可得“根的判别式△=0”，从而可得关于m的方程，解方程求得m的值，代入原方程可求得方程的两根，再由三角形三边之间的关系检验即可.

    试题解析：

    (1)(x1－1)(x2－1)＝28，即x1x2－(x1＋x2)＝27，而x1＋x2＝2(m＋1)，x1x2＝m2＋5，

    ∴m2＋5－2(m＋1)＝27，

    解得m1＝6，m2＝－4，

    又Δ＝[－2(m＋1)]2－4×1×(m2＋5)≥0时，m≥2，

    ∴m的值为6;　

    (2) 若7为腰长，则方程x2－2(m＋1)x＋m2＋5＝0的一根为7，

    即72－2×7×(m＋1)＋m2＋5＝0，

    解得m1＝10，m2＝4，

    当m＝10时，方程x2－22x＋105＝0，根为x1＝15，x2＝7，不符合题意，舍去．

    当m＝4时，方程为x2－10x＋21＝0，根为x1＝3，x2＝7，此时周长为7＋7＋3＝17　

    若7为底边，则方程x2－2(m＋1)x＋m2＋5＝0有两等根，

    ∴Δ＝0，解得m＝2，此时方程为x2－6x＋9＝0，根为x1＝3，x2＝3，3＋3<7，不成立，

    综上所述，三角形周长为17

    点睛：（1）一元二次方程根与系数的关系成立的前提条件是方程要有实数根，即“根的判别式△ ”；（2）涉及三角形边长的问题中，解得的结果都需要用“三角形三边之间的关系”检验，看三条线段能否围成三角形.

    【题型】解答题
    【结束】
    21

    【题目】如图，已知在△ABC中，D是AB的中点，且∠ACD=∠B，若 AB=10，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将△ABC绕点B逆时针旋转α得到△DBE，DE的延长线与AC相交于点F，连接DA、BF．

    （1）如图1，若∠ABC=α=60°，BF=AF．

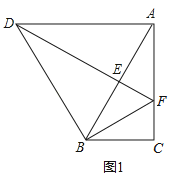
    ①求证：DA∥BC；②猜想线段DF、AF的数量关系，并证明你的猜想；

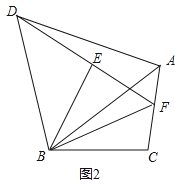
    （2）如图2，若∠ABC＜α，BF=mAF（m为常数），求的值（用含m、α的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B＝135°，P′A∶P′C＝1∶3，则P′A∶PB＝( )

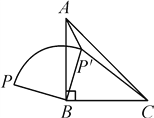
    A. 1∶ B. 1∶2 C. ∶2 D. 1∶

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，对称轴为直线.下列结论中，正确的是（　　）

    A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一次函数y=kx+b的自变量x的取值范围是-2≤x≤6，相应的函数值的范围是-11≤y≤9，求此函数的表达式．

    查看答案和解析>>

    同步练习册答案