
【题目】如图, ![]() 在平面直角坐标系中,在正方形网格中,每个小正方形的边长为 1 个单位长度
在平面直角坐标系中,在正方形网格中,每个小正方形的边长为 1 个单位长度
(1)画出将![]() 向下平移 4 个单位长度后得到的
向下平移 4 个单位长度后得到的![]() ;
;
(2)画出将![]() 绕点 C 逆时针方向旋转
绕点 C 逆时针方向旋转![]() 得到的
得到的![]() ;
;
(3)在(2)的条件下,求线段![]() 旋转到
旋转到![]() 扫过的面积(结果保留
扫过的面积(结果保留![]() )
)

科目:初中数学 来源: 题型:
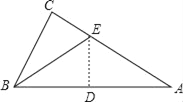
【题目】有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( )
A. 2![]() B.
B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
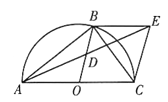
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,且点
上一点,且点![]() 不与点
不与点![]() 重合,点
重合,点![]() 为半径
为半径![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:点![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行职工五人制足球联赛,共赛 17 轮(即每队均需参赛 17 场),记分办法是胜一场得 3分,平一场得 1 分,负一场得 0 分 . 若![]() 足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算
足球队总积分为 16 分,且踢平场数是所负场数的整数倍,试推算![]() 足球队所负场数的情况有( )
足球队所负场数的情况有( )
A.1 种B.2 种C.3 种D.4 种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某电暖科技有限公司准备购进A型(直热式电暖)和B型(智能电风幕电暖)两种设备,经计算,购进 3 台A设备和 2 台B设备需用 6.6 万元,购进 1 台A设备和 3 台B设备需用5. 7 万元 .
请解答下列问题:
(1)求A、B两种设备的进价;
(2)该公司计划用 21 万元同时购进A、B两种设备,若A设备以每台1.5万元的价格出售,B设备以每台2万元的价格出售,且全部售出,请求出所获利润W(单位:万元)与购买A设备的资金m(单位:万元)之间的函数关系式;
(3)在(2)的条件下,要求A设备的利润不低于B设备的利润,并将(2)中的最大利润全部用于购买甲(小米笔记本4000元/台)、乙(华为笔记本6000元/台)两种型号的电脑赠给某中学,请求出有几种购买电脑的方案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.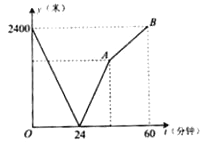
(1)根据图象信息,当t=________分钟时甲乙两人相遇,甲的速度为________米/分钟;
(2)求出线段AB所表示的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有五张背面相同的卡片,正面分别印有圆、矩形、等边三角形、菱形、平行四边形(邻边不相等且不垂直),现将五张卡片正面朝下洗匀任意摆放,从中随机抽取两张,抽到的两张卡片上都恰好印的既是中心对称又是轴对称的图形的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.

(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com