
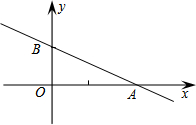
 如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$.
如图,在以点O为原点的直角坐标系中,一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=$\frac{1}{2}$AB,反比例函数y=$\frac{k}{x}$的图象经过点C,则k的值为-$\frac{11}{50}$. 分析 首先求出点A、B的坐标,然后由勾股定理求得AB,设∠BAO=θ,则sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$,过点O作Rt△AOB斜边上的高OE,斜边上的中线OF,通过解直角三角形求得AE=OA•cosθ=2×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$,根据三角形中线的性质求得OF=$\frac{1}{2}$AB,从而求得OC=OF=$\frac{\sqrt{5}}{2}$,进而求得AC=AE+EC=$\frac{4\sqrt{5}}{5}$+$\frac{3\sqrt{5}}{10}$=$\frac{11\sqrt{5}}{10}$.过点C作CG⊥x轴于点G,则CG=AC•sinθ=$\frac{11\sqrt{5}}{10}$×$\frac{\sqrt{5}}{5}$=$\frac{11}{10}$,AG=AC•cosθ=$\frac{11\sqrt{5}}{10}$×$\frac{2\sqrt{5}}{5}$=$\frac{11}{5}$,从而求得C的坐标,然后根据待定系数法即可求得.
解答 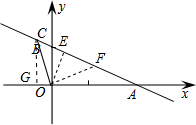 解:如图,在y=-$\frac{1}{2}$x+1中,令y=0,则x=2;令x=0,得y=1,
解:如图,在y=-$\frac{1}{2}$x+1中,令y=0,则x=2;令x=0,得y=1,
∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB=$\sqrt{5}$.
设∠BAO=θ,则sinθ=$\frac{\sqrt{5}}{5}$,cosθ=$\frac{2\sqrt{5}}{5}$.
过点O作Rt△AOB斜边上的高OE,斜边上的中线OF,则AE=OA•cosθ=2×$\frac{2\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$,OF=$\frac{1}{2}$AB,
∵OC=$\frac{1}{2}$AB,
∴OC=OF=$\frac{\sqrt{5}}{2}$,
∴EF=AE-AF=$\frac{4\sqrt{5}}{5}$-$\frac{\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{10}$.
∵OC=OF,OE⊥CF,
∴EC=EF=$\frac{3\sqrt{5}}{10}$,
∴AC=AE+EC=$\frac{4\sqrt{5}}{5}$+$\frac{3\sqrt{5}}{10}$=$\frac{11\sqrt{5}}{10}$.
过点C作CG⊥x轴于点G,则CG=AC•sinθ=$\frac{11\sqrt{5}}{10}$×$\frac{\sqrt{5}}{5}$=$\frac{11}{10}$,
AG=AC•cosθ=$\frac{11\sqrt{5}}{10}$×$\frac{2\sqrt{5}}{5}$=$\frac{11}{5}$,
∴OG=AG-OA=$\frac{11}{5}$-2=$\frac{1}{5}$.
∴C(-$\frac{1}{5}$,$\frac{11}{10}$).
∵反比例函数y=$\frac{k}{x}$的图象经过点C,
∴k=-$\frac{1}{5}$×$\frac{11}{10}$=-$\frac{11}{50}$,
故答案为-$\frac{11}{50}$.
点评 本题考查了反比例函数与一次函数的交点问题,其知识点:勾股定理的应用,解直角三角形,直角三角形斜边中线的性质,待定系数法求解析式等.


 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
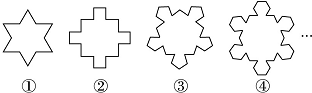
| A. | n(n-1) | B. | n(n+1) | C. | (n+1)(n-1) | D. | n2+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
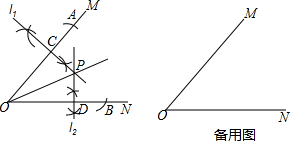
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
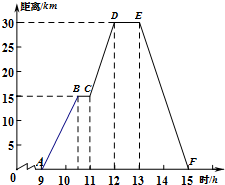 小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )
小强骑自行车去郊游,9时出发,15时返回.右图表示他距家的距离y(千米)与相应的时刻x(时)之间的函数关系的图象.根据这个图象,小强14时距家的距离是( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com