
分析 (1)由题意可知:菱形ABCD的边长是5,则AO2+BO2=25,则再根据根与系数的关系可得:AO+BO=-2m+1,AO•BO=m2+3;代入AO2+BO2中,得到关于m的方程后,求得m的值;
(2)将m的值代入方程求得OA、OB的值,最后根据菱形的面积=△AOB面积的4倍求解即可.
解答 解:(1)由直角三角形的三边关系可得:AO2+BO2=25,由根与系数的关系可得:AO+BO=-2m+1,AO•BO=m2+3,
∴AO2+BO2=(AO+BO)2-2AO•BO=(-2m+1)2-2(m2+3)=25,整理得:m2-2m-15=0,解得:m=-3或5.
又∵△>0,
∴(2m-1)2-4(m2+3)>0,
解得m<-$\frac{11}{4}$,
∴m=-3.
(2)将m的值代入方程得;x2-7x+12=0.
解得x1=3,x2=4.
∴菱形ABCD的面积=4×$\frac{1}{2}OA•OB$=4×$\frac{1}{2}×3×4$=24.
点评 本题主要考查的是菱形的性质、勾股定理、根与系数的关系的综合应用,由AO2+BO2=(AO+BO)2-2AO•BO列出关于m的方程是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 a,b为有理数,且a+b,a-b在数轴上如图所示:
a,b为有理数,且a+b,a-b在数轴上如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,0) | B. | (-5,0) | C. | (3,0)或(-5,0) | D. | (-1,0)或(5,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
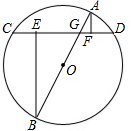 如图,AB是⊙O的直径,弦CD与AB相交于点G,过点A,B分别向弦CD作垂线,垂足分别为F、E
如图,AB是⊙O的直径,弦CD与AB相交于点G,过点A,B分别向弦CD作垂线,垂足分别为F、E查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{x}$÷$\frac{x}{3}$=$\frac{9}{x}$ | B. | ($\frac{1}{x-3}-\frac{x+1}{{x}^{2}-1}$)•(x-3)=$\frac{2}{x-1}$ | ||
| C. | ($\frac{a}{a-2}-\frac{a}{a+2}$)•$\frac{4-{a}^{2}}{a}$=4 | D. | ($\frac{{b}^{2}}{a+b}-\frac{{a}^{2}}{a+b}$)•$\frac{ab}{a-b}$=ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com