
【题目】如图1,二次函数y=ax2+bx+3 ![]() 经过点A(3,0),G(﹣1,0)两点.
经过点A(3,0),G(﹣1,0)两点.
(1)求这个二次函数的解析式;
(2)若点M时抛物线在第一象限图象上的一点,求△ABM面积的最大值;
(3)抛物线的对称轴交x轴于点P,过点E(0, ![]() )作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
)作x轴的平行线,交AB于点F,是否存在着点Q,使得△FEQ∽△BEP?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:将A、G点坐标代入函数解析式,得
![]() ,
,
解得 ![]() ,
,
抛物线的解析式为y=﹣ ![]() x2+2
x2+2 ![]() x+3
x+3 ![]()
(2)解:作ME⊥x轴交AB于E点,如图1
 ,
,
当x=0时,y=3 ![]() ,即B点坐标为(0,3
,即B点坐标为(0,3 ![]() )
)
直线AB的解析式为y=﹣ ![]() x+3
x+3 ![]() ,
,
设M(n,﹣ ![]() n2+2
n2+2 ![]() n+3
n+3 ![]() ),E(n,﹣
),E(n,﹣ ![]() n+3
n+3 ![]() ),
),
ME═﹣ ![]() n2+2
n2+2 ![]() n+3
n+3 ![]() ﹣(﹣
﹣(﹣ ![]() n+3
n+3 ![]() )=﹣
)=﹣ ![]() n2+5
n2+5 ![]() n,
n,
S△ABM= ![]() MExA=
MExA= ![]() (﹣
(﹣ ![]() n2+5
n2+5 ![]() n)×3=﹣
n)×3=﹣ ![]() (n﹣
(n﹣ ![]() )2+
)2+ ![]() ,
,
当n= ![]() 时,△ABM面积的最大值是
时,△ABM面积的最大值是 ![]()
(3)解:存在;理由如下:
OE= ![]() ,AP=2,OP=1,BE=3
,AP=2,OP=1,BE=3 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当y= ![]() 时,﹣
时,﹣ ![]() x+3
x+3 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,即EF=
,即EF= ![]()
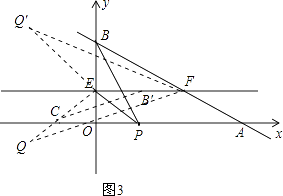
将△BEP绕点E顺时针方向旋转90°,得到△B'EC(如图3),
∵OB⊥EF,
∴点B'在直线EF上,
∵C点横坐标绝对值等于EO长度,C点纵坐标绝对值等于EO﹣PO长度,
∴C点坐标为(﹣ ![]() ,
, ![]() ﹣1),
﹣1),
过F作FQ∥B'C,交EC于点Q,
则△FEQ∽△B'EC,
由 ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
可得Q的坐标为(﹣ ![]() ,﹣
,﹣ ![]() );
);
根据对称性可得,Q关于直线EF的对称点Q'(﹣ ![]() ,
, ![]() )也符合条件.
)也符合条件.
【解析】(1)根据待定系数法,可得函数解析式;(2)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得ME的长,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案.(3)即可确定△BEP,根据相似三角形的判定定理即可求得点Q的坐标,解题时要注意答案的不唯一性.


科目:初中数学 来源: 题型:
【题目】(1)计算:﹣12018﹣|﹣2|÷![]() ;
;
(2)先化简,再求值:6ab﹣[2(a2+ab﹣![]() )﹣3(a2﹣2ab+b2)﹣1],其中a=﹣1,b=
)﹣3(a2﹣2ab+b2)﹣1],其中a=﹣1,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在,某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果红旗商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:因为:∠A=∠F,
所以:_____//______,
理由是:____________,
所以:∠____+∠_____=180°,
理由是:_______________,
因为:∠C=∠D,
所以∠D+∠DEC=180°,
理由是:_________________,
所以:______________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
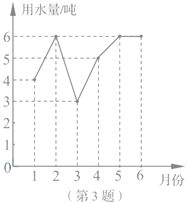
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com